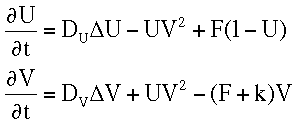Moving-grid methods
Paul Zegeling
What are moving-grid methods?
Moving-grid methods are solution-adaptive methods for time-dependent
partial differential equations (PDEs). These methods, also characterized by
the terms r-refinement (*), continuously deforming grids, or dynamically
moving grids, move the spatial grid continuously in time while the
discretization of the PDE and the grid selection procedure are intrinsically
coupled.
-
(*) h-refinement methods ('local refinement') adapt the grid only at
discrete time levels, whereas p-refinement methods (mostly of finite-element
type) increase or decrease the order of approximation where, when and if
necessary. In advanced applications also hybrid methods exist:
h-p-, h-r-, or r-p-refinement.
Moving-grid methods use a fixed number of spatial grid points, without need
of interpolation, and let them move with "whatever fronts are present".
Using these methods, if properly applied, can save up to a factor of 10 (in 1D)
or 100 (in 2D) spatial grid points in the case of steep moving layers
stemming from a convection-diffusion or reaction-diffusion system.
Comparison of a fixed grid with a moving grid
The following four pictures illustrate the difference between fixed grid and moving grid methods for the one-dimensional Burger's equation.
[4 pictures, 21 kB in total]
The following movie shows a uniform non-moving central-difference scheme for a two-dimensional Burgers' type equation :
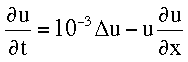
[mpeg-movie, 351 kB]
Grid degeneration
An intrinsic difficulty of topological nature exists: so-called
`grid distortion' or `grid degeneration'. In terms of transformation of
variables (non-uniform in (x,y,t) -> uniform ( )) this means that for some instances the Jacobian may become zero or almost zero.
)) this means that for some instances the Jacobian may become zero or almost zero.
The following pictures show three possible cases of grid degeneration.
[3 pictures, 27 kB in total]
Applications
An interesting application of a moving-grid method in 1D can be found
in a tidally-averaged advection-dispersion model.
Application of the same method to a `lava-dome' model can be found in
lava-dome model.
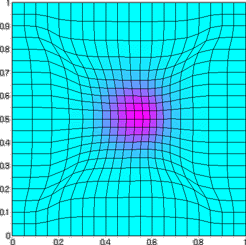
Recent work by the author dealing with moving grids concerns the application
to the Gray-Scott reaction-diffusion model, which describes two
irreversible chemical reactions. The PDE-system reads :
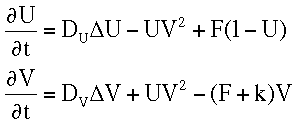
where k is the dimensionless rate constant of the second reaction and
F is the dimensionless feed rate. It is known from experiments that
many different complex patterns (regular, stationary, periodic, chaotic)
can be found for different choices of the parameters.
Even in one space dimension interesting solution behaviour may occur for
which moving-grid methods could be benificial.
Self replicating patterns in 1D
For the 1D-case a moving-finite-difference method based on equidistribution
(with spatial and temporal smoothing) is used to detect the splitting of the
pulses.
Self-replicating patterns recognized by moving grids :
[gif, 76 kB]
Irregular solution behaviour created by changing the parameters :
[gif, 72 kB]
Self replicating patterns in 2D
For the 2D-case a moving-finite-element method based on minimizing the
PDE-residual (with regularization) gives:
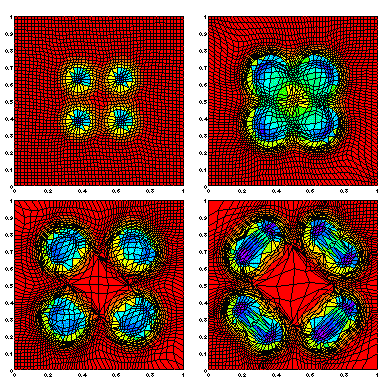
The following movie shows the U-component of another pattern in two dimensions (a "moving vulcano"):
[mpeg-movie, 1.5 MB]
Moving Finite Differences in 2D
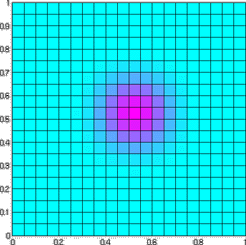
Below you find some results obtained by a moving finite difference method in two space dimensions, which is based on
smoothed equidistribution. It is applied to a 2D Burgers'
equation.
>
Moving-finite-differences (N=21) for Burgers' equation at t=0, t=0.1 :
Many references on this subject can be found [HERE]
Other interesting pages:
Gradient-weighted moving-finite-elements:
Neil Carlson, Purdue University (also 3D!).
Moving-finite-elements:
Mike Baines,
University of Reading.
Moving-finite-volumes:
John Mackenzie, Strathclyde University.
Moving-mesh-PDEs:
Weizhang Huang, University of Kansas;
and Bob Russell, Simon Fraser University.
The method-of-lines and adaptive grids:
Bill Schiesser, Lehigh University.
Moving grids with the deformation method:
Guojun Liao, Univ. of Texas
at Arlington.
Application of moving grids to PDE models with Boussinesq convection (also movies):
Hector Ceniceros, Univ. of California (Santa Barbara).
Moving grids and harmonic maps:
Tang Tao, Hong Kong Baptist University.
Books on adaptive grids and grid generation
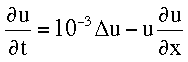
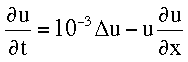
 )) this means that for some instances the Jacobian may become zero or almost zero.
)) this means that for some instances the Jacobian may become zero or almost zero.