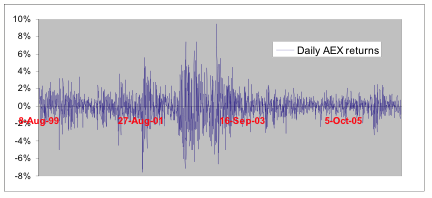
Figure 1: Daily returns on the AEX stock index for August 1999 - December 2006.


Volatility, i.e., the uncertain fluctuations in the prices of financial assets such as stocks, is of paramount importance in financial markets theory and practice. Volatility characterizes the risk of an investment. Moreover, volatility is a major determinant of the price of a financial derivative.
A financial derivative is a contract that derives its value from another, underlying asset. The holder of a call option for example, has the right (but not the obligation) to buy stock for a certain contract-specified price, the strike price, at some date in the future, the expiration date. A put option gives the right to sell. The value of this right is given by the option price.
Apart from these so-called vanilla calls and puts, numerous other option-style products are traded in today's financial markets. These assets are collectively dubbed exotic options. Nowadays, a multimillion industry in these derivatives exists, and financial engineers continually invent new products to extend a bank's product range. These products are often tailored to the specific needs of a bank's clients and are typically sold over the counter, rather than at organized markets.
A bank or other financial institution wishing to issue a new derivative wants to know the fair price that can be asked for this product. A derivative pricing model serves this purpose.

Figure 1: Daily returns on the AEX stock index for August 1999 - December 2006.
In practice, the most widely applied model is still the celebrated Black-Scholes (1973) model, in which the underlying stock price follows geometric Brownian motion. The main advantage of the Black-Scholes (BS) model is that it leads to analytical (i.e. closed-form) formulas for many of the standard option contracts (the famous Black-Scholes formula). The BS model depends on just one unknown parameter, the underlying stock volatility, which the model assumes constant. As such, once this volatility has been estimated from e.g. vanilla option data, any exotic option can subsequently be priced by numerical techniques, such as Monte Carlo simulation.
As convenient as this is, the Black-Scholes model is severely misspecified. Volatility changes over time, volatility is stochastic. Periods of high and low stock volatility alternate in the practice of financial markets, a phenomenon known as volatility clustering. Figure 1 illustrates this phenomenon. It plots the daily returns on the AEX stock index for the period August 1999 - December 2006. Note that the spread in the return realizations (i.e. volatility) is not constant.
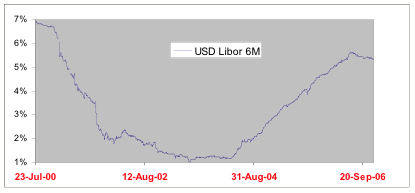
Figure 2: Evolution of the 6-month LIBOR interest rate for July 2000 - Dec 2006.
A more realistic model in this respect is the Heston (1993) model. The Heston model assumes that both the underlying stock price and its volatility evolve randomly over time.
A remaining drawback of the conventional Heston model is its assumption of constant interest rates. This assumption is empirically violated, as figure 2 illustrates. Interest rates change randomly over time as well. (Indeed, in practice there exists an enormous market in so-called interest rate derivatives, which derive their value from the random evolution of certain interest rates.)
As both stochastic volatility and stochastic interest rates provide a more realistic data description, a derivative pricing model in which both features are explicitly modeled has a clear potential of generating more accurate exotic option prices.
ING currently aims at extending its range of derivative pricing models by a desire to implement a Heston-type model that incorporates stochastic interest rates. The interest rate and stock price fluctuations are allowed to be correlated.
Although the theoretical framework is more or less clear-cut, the challenge lies in a practical implementation of this “hybrid” Heston model. This will be clarified shortly.
All derivative pricing models depend on unknown parameters. Before a model can be used for pricing exotic options, its parameters need to be estimated. This is typically done by extracting information from the prices of vanilla options, which are observed in the market.
A commonly applied estimation method is calibration. Calibration performs parameter estimation by minimizing the sum of squared deviations between the market-observed and theoretical vanilla option prices on a particular day, essentially by a (computationally intensive) non-linear least squares procedure. In the calibration procedure, it is important that vanilla option prices can both be rapidly and accurately computed.
A rather recently derived pricing formula for vanilla options involves the characteristic function of the (log) stock price process. Importantly, this formula applies irrespective of the specific dynamics assumed for the underlying stock price evolution.
An important advantage of this is that the option pricing routine that ING has implemented, only needs as input the characteristic function associated with the assumed dynamics for the stock price. If e.g. a trader likes to switch to another pricing model, only the corresponding characteristic function needs to be changed, whereas the actual calibration/pricing algorithm remains untouched. As there exists no best option pricing model, this allows the trader to easily compare the exotic option prices generated by different models.
For many well-known derivative pricing models, the characteristic function of the log-stock price process is known analytically (i.e. in closed form). This includes the Black-Scholes and Heston models amongst others.
For the hybrid Heston model with stochastic interest rates,
If this is indeed the case,
If this is not the case,
This would allow ING to calibrate the hybrid Heston model to vanilla option prices (and interest rate derivatives), and subsequently price exotic options consistently, in a world with both stochastic volatility and stochastic interest rates.