wiskonst.nl

In de vlakke meetkunde bestudeert men vormen in het vlak en hun eigenschappen. Het is een van de oudste takken van de wiskunde en het is ook de tak van de wiskunde die in de oudheid het meest ontwikkeld was. Veel van de belangrijke stellingen en technieken stammen uit de oudheid.

De klassieke meetkunde hield zich hoofdzakelijk bezig met vraagstukken over lijnen en cirkels. Een belangrijk thema bestaat uit constructies met passer en lineaal. Dit is een meetkundige lineaal: hij heeft geen schaalverdeling, het is dus enkel een instrument om een rechte lijn tussen twee punten te trekken. De passer kan ook niet gebruikt worden om afstanden "over te brengen", maar alleen om een cirkel te tekenen met een bekend middelpunt en een bekend punt op de rand.

Typische constructieproblemen zijn bijvoorbeeld het vinden van het midden van een gegeven lijnstuk of het construeren van de bisectrice van een gegeven hoek.

De eerste hiervan lossen we als volgt op.

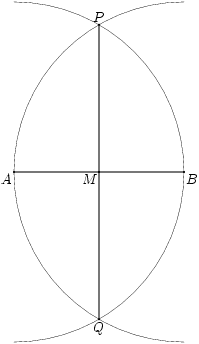
We tekenen de cirkel met middelpunt A en B op de omtrek, alsmede de cirkel met middelpunt B en A op de omtrek. De snijpunten van deze cirkels noemen we P en Q. De lijn door P en Q snijdt het lijnstuk AB nu precies in het midden M.

Voor de constructie van een bisectrice gaan we als volgt te werk.

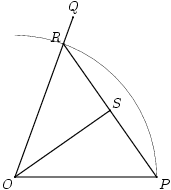
De hoek die we doormidden willen delen is hoek POQ. We tekenen de cirkel met O als middelpunt en P op de straal. Deze snijdt de lijn door O en Q in het punt R. Het midden S van lijnstuk PR ligt nu op de bisectrice van hoek POQ. Dus de gezochte bisectrice is de lijn door O en S.

Binnen de klassieke meetkunde werkt men hoofdzakelijk met grootheden; lengten, oppervlakten en inhouden. Dit zijn niet gewoon getallen, werschillende soorten grootheden zijn niet met elkaar te vergelijken: een lijn plus een vlak 'is niets', dus mag je nooit een lijn en een vlak bij elkaar optellen. Je mag wel, bijvoorbeeld, twee lijnen met elkaar vermenigvuldigen tot een vlak. Je loopt nu tegen problemen op als je twee vlakken met elkaar wilt vermenigvuldigen: vlak × vlak 'bestaat immers niet', dus kunnen we er niet mee werken.

Verhoudingen spelen een belangrijke maar ingewikkelde rol in klassieke meetkunde: je mag bijvoorbeeld een verhouding tussen twee lijnen vergelijken met een verhouding tussen twee vlakken, hoewel je lijnen en vlakken niet direct met elkaar kunt vergelijken. Zo weet je bijvoorbeeld dat, als twee driehoeken dezelfde hoogte hebben, de oppervlakten zich net zo verhouden als de lengten van de bases. Let wel dat een verhouding geen getal is. A staat tot B is vijf mag niet. Wel mag je zeggen dat A staat tot B hetzelfde is als C staat tot D.

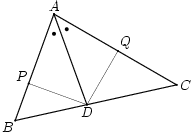
Als een voorbeeld kijken we naar de bisectricestelling. Begin met een driehoek ABC en laat AD de bisectrice van hoek BAC. Dan geldt dat AB:AC gelijk is aan DB:DC.

Om dit te bewijzen gaan we als volgt te werk. Laat P en Q de voetpunten van de loodlijnen door Q op AB resp. AC. Deze lijnen even lang, immers driehoeken ADP en ADQ hebben dezelfde hoeken en zijn dus congruent, bovendien hebben ze de zijde AD gemeenschappelijk en zijn dus zelfs gelijkvormig. Bij gevolg verhouden de oppervlaktes van de driehoeken ADB en ADC zich als AB en AC. Kijken we op een andere manier naar dezelfde driehoeken dan zien we dat ze alletwee A als top en basis op de lijn BC hebben. De oppervlaktes verhouden zich dus ook als de lengtes van deze bases, dat wil zeggen, DB en DC.

Het heeft lang geduurd voordat er echt nieuwe wiskunde werd ontdekt binnen de vlakke meetkunde. De eerste technieken die de klassieke methoden echt voorbijstreven zijn die van Descartes' analytische meetkunde.

In de Cartesische meetkunde kies je een eenheidslengte en daardoor is het plotseling mogelijk om met lengten te rekenen alsof het echt getallen zijn. Een product van twee lengtes kan bijvoorbeeld weer een lengte zijn, zoals in het volgende plaatje.

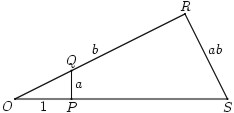
Het lijnstuk OP heeft lengte 1 (de gekozen eenheidslengte). De lijnstukken PQ en OR hebben de twee lengten die we met elkaar willen vermenigvuldigen. De bewering is dat het lijnstuk RS de lengte van dit product heeft. De driehoeken OPQ en ORS zijn immers congruent, zodat de verhouding OP:PQ gelijk is aan OR:RS, oftewel 1:a = b:RS, zodat we zien dat RS inderdaad lengte a×b heeft.

Door en eenheidslengte te kiezen kun je verhoudingen, en daarmee gewone getallen, vertalen naar lengten: je kunt het getal vijf gelijkstellen aan een lengte die vijf keer zo lang is als de eenheidslengte. Om dat je getallen kunt vermenigvuldigen kan je nu effectief lengten ook met elkaar vermenigvuldigen, zo dat er een lengte uit komt in plaats van een oppervlakte.

Om een meetkundig probleem op te lossen gaat Descartes als volgt te werk: Hij geeft iedere bekende en onbekende grootheid in de figuur een naam (of letter) en vertaalt hun meetkundige eigenschappen naar algebraïsche relaties die gelden tussen deze variabelen. Het oplossen van het probleem komt nu neer op het manipuleren van deze vergelijkingen, zo dat er een vergelijking uit komt die je oplossing beschrijft. Vervolgens kan je de vergelijking bestuderen om te kijken wat voor meetkundige figuur er bij de oplossing hoort.

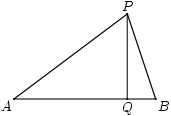
Tijd voor een voorbeeld. Begin met twee punten A en B. De middelloodlijn van het lijnstuk AB heeft de eigenschap dat elk punt erop even ver van A als van B af ligt. We vragen ons nu af hoe de verzameling van alle punten die twee keer zo ver van A als van B af liggen er uit ziet. Bekijk het plaatje.

In het plaatje zijn A en B de gegeven punten en is P een punt met de gewenste eigenschap. We laten een loodlijn neer vanuit P op AB, het voetpunt noemen we Q. We bepalen nu aan welke voorwaarden P moet voldoen. We voeren variabelen in voor diverse grootheden: laat d de lengte van AB, x die van AQ, y die van QP, u die van AP en v die van BP. We willen nu dat u gelijk is aan 2v. Vanwege de stelling van Pythagoras weten we ook dat u2 = x2 + y2 en v2 = (d-x)2 + y2.

x2 + y2 = 4((d-x)2 + y2).

Een veelvoud aan herschrijvingen later krijgen we de vergelijking

(x - 4/3d)2 + y2 = (2/3d)2.

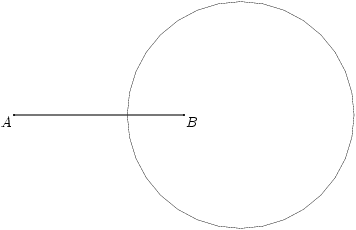
Hierin zien we dat de oplossing een cirkel is met middelpunt y = 0, x = 4/3d en straal 2/3d. Dit geeft het volgende plaatje.

In het bovenstaande voorbeeld hebben we gezien hoe de analytische meetkunde te werk gaat bij het oplossen van een probleem. We zoeken een algebraïsche vergelijking die de meetkundige eigenschappen van het gezochte punt weergeeft. Het grote probleem van deze methode is dat het meestal niet makkelijk of zelfs niet mogelijk is om de meetkundige figuur te vinden die hoort bij de gevonden vergelijking.