Een groot deel van Descartes' 'la Geometrie' wordt besteed aan het uitwerken van 'een probleem, getrokken uit Pappus'. Dit probleem neemt een stuk van het eerste deel en heel deel 2 in beslag.We zullen op deze pagina uitleggen wat het probleem is, en hoe Descartes het heeft op gelost.
Probleem getrokken uit Pappus
Aanpassing: het probleem met alleen rechte hoeken
Voorbeeld van de klassieke methode
Analytische meetkunde
Voorbeeld van de methode van Descartes
Samenvatting
Probleem getrokken uit Pappus
Dit zogeheten 'probleem getrokken uit Pappus' is niet van Pappus. Descartes noemt het zo omdat de wiskundige Pappus van Alexandrië rond 340 na Christus een boek heeft geschreven waarin hij een overzicht geeft van wat alle wiskundige resultaten die hij kent. Hij behandelt hier ook diverse problemen die hij niet op kan lossen. Veel van deze problemen worden aangeduid als 'een probleem van Pappus', omdat Pappus' boek de oudste bewaarde bron is waar het desbetreffende probleem in staat. Andere bekende 'problemen van Pappus' gaan onder andere over de eigenschappen van de hoekpunten van een zeshoek, en de inhoud van een de figuur die je krijgt door een kromme rond een as te wentelen.
Zoals gezegd heeft Pappus dit probleem nooit opgelost. Hij zegt in zijn boek zelfs expliciet dat noch Apollonius, noch Euclides (beiden beroemde wiskundigen uit het oude Griekenland) het probleem hebben kunnen oplossen. Descartes wil laten zien dat hij dit probleem wel aankan met zijn 'nieuwe meetkunde'. Dit dient twee doelen: hij kan een voorbeeld geven van hoe zijn methode werkt, en hij heeft een manier om zijn rare meetkunde verkopen aan zijn tijdgenoten. Door te laten zien dat hij dingen kan doen die niet voor mogelijk werden gehouden hoopte Descartes dat zijn mede-wiskundigen zouden inzien hoe goed zijn 'nieuwe meetkunde' was.
We zullen later laten zien wat de grote revolutie van Descartes' 'nieuwe meetkunde' precies inhoudt. Eerst bespreken we het 'probleem getrokken uit Pappus', en geven we een paar voorbeelden.
Wat is nu het probleem?
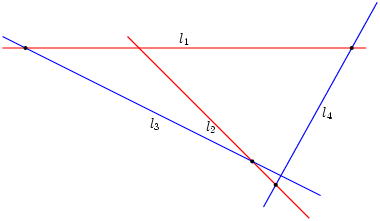
Gegeven is een even aantal lijnen in het platte vlak, l1 tot en met ln. Bij iedere lijn is een hoek gegeven: bij de lijn li hoort de hoek αi. Gegeven is ook een punt c in het platte vlak. Let op: bijna alle lijnen waar we het over zullen hebben zijn meetkundige lijnen! Dat wil zeggen dat ze oneindig lang zijn naar allebei de kanten. In de plaatjes hebben we lijnen die ophouden, maar je moet in gedachten houden dat de lijnen gewoon doorlopen.
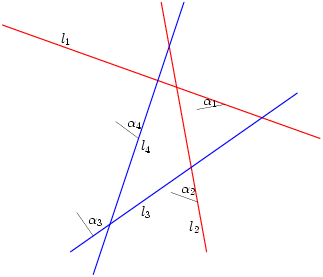
Lijnen l1 t/m l4, iedere met een bijbehorende hoek.
We kunnen nu vanuit c een lijn m1 trekken die lijn l1 snijdt onder hoek α1 (een makkelijke manier om te laten zien dat dit altijd kan: Je kunt een willekeurige lijn tekenen die l1 snijdt met hoek α1. Je kunt deze lijn nu langs l1 schuiven tot c er precies op ligt.). Op dezelfde manier kun je lijnen m2 t/m mn trekken, die allemaal door c heengaan en lijn li snijden met hoek αi.
Je hebt nu een aantal lijnstukken die van c naar de snijpunten van de li en mi lopen. Noem deze lijnstukken di. Deze di zijn lijnstukken, en geen oneindig lange lijnen. Ze lopen dus tussen twee eindpunten, en hebben daarom een lengte die we kunnen uitrekenen.
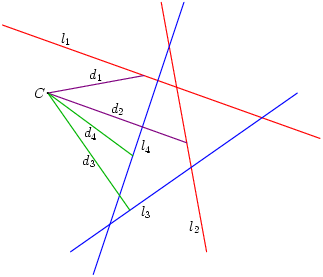
De lijnen mi , met de afstanden di.
Het probleem getrokken uit Pappus gaat over de verhoudingen van deze di. Om precies te zijn: De di worden verdeeld in twee groepen van gelijke grootte, en alle di in iedere groep worden met elkaar vermenigvuldigd. De vraag is voor welke punten c deze producten gelijk zijn.
In het bovenstaande plaatje kunnen we bijvoorbeeld de vraag stellen wanneer d1×d4 gelijk is aan d2×d3. Voor een ingewikkelder probleem kunnen we bijvoorbeeld zeven lijnen nemen, en ons afvragen wanneer d1×d3×d5×d7 gelijk is aan d2×d4×d6.
Aanpassing: het probleem met alleen rechte hoeken
In het oorspronkelijke probleem mogen alle hoeken verschillend zijn. Het is echter voor het verdere reken- en tekenwerk erg prettig als alle hoeken 90 graden zijn. Is er een manier om het probleem zo te veranderen dat we hoeken van 90 graden mogen gebruiken?
Ja, dat kan.
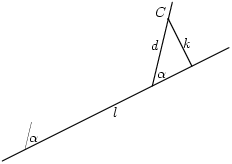
Hierboven zie je een lijn l, met een gegeven hoek α en een punt c. Je ziet ook het standaard lijnstuk met lengte d, en de loodlijn k door c op l. Hoe lang is k?
Met elementaire meetkunde kun je zie dat k = d/sinus(α). Omdat sinus(α) overal constant is (α is immers gegeven) kunnen we zeggen dat k = b×d, met b een constante.
Deze redenering gaat natuurlijk op voor alle li. We kunnen dus alle ki schrijven als bi×di. De vergelijking d1×d2 = d3×d4 wordt dan: b1×k1×b2×k2 = b3×k3×b4×k4. Oftewel: k1×k2 = B×k3×k4, met B de constante gelijk aan (b3×b4)/(b1×b2).
Als we het probleem uitbreiden naar k1×...×ki = B×kj×...×kk mogen we aannemen dat alle hoeken recht zijn. We zullen later laten zien dat het rekenen met de constante B minder moeilijk is dan het rekenen met allerlei verschillende hoeken.
Voorbeeld van de klassieke methode
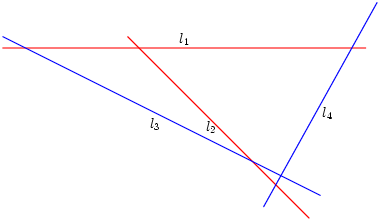
We nemen weer vier lijnen, l1 t/m l4. Om het voorbeeld simpel te houden kiezen we all hoeken αi recht, zodat B = 1 in de bovenstaande berekening.
Het probleem dat we willen oplossen is: "Voor welke punten c geldt dat d1×d2 = d3×d4?".
Hoe gaan we dit oplossen?
Dit probleem is op te lossen met klassieke meetkunde, maar dat is bijzonder moeilijk. Als we meer lijnen toevoegen is het met klassiek meetkunde zelfs helemaal niet meer op te lossen. Je kunt de oplossingsverzameling dan niet meer tekenen met passer en lineaal (probeer bijvoorbeeld maar eens een derdemachtsfunctie precies te tekenen!). We kunnen daarentegen wel een heel eind komen met klassieke meetkunde, en door dat te doen krijgen we beter inzicht in het probleem. We zullen laten zien wat je wel en niet kunt met passer en lineaal, laten zien hoe je het probleem volledig op kunt lossen met behulp van analytische meetkunde, en een goed te volgen voorbeeld geven.
Een paar makkelijke punten
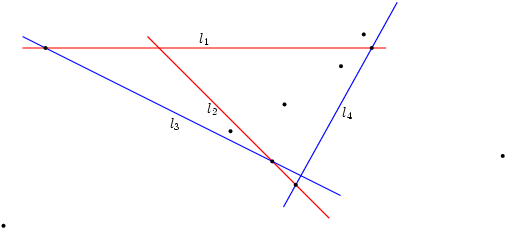
We kunnen met een beetje redeneren al een aantal punten vinden: Kies het punt waar l1 l3 snijdt. Hier geldt: d1 = d3 = 0. Dus geldt d1×d2 = d3×d4 = 0, en is dit een van de punten die we zoeken. Op dezelfde manier geven de snijpunten van l1 en l4, l2 en l3 en l2 en l4 punten waar de vergelijking geldt. In het onderstaande plaatje zie je dat we al 4 punten van de oplossing hebben!
Een gevolg hiervan is dat de enige punten op de lijn li die voldoen aan de vergelijking de snijpunten met lijnen uit de 'andere groep' zijn. Op de lijn li is de afstand di immers 0, en daarmee de vermenigvuldiging waar di in zit ook. De enige manier waarop de vergelijking dan nog kan kloppen is als de andere kant van de vergelijking ook 0 is, doordat een van de dj aan die kant nul is. Maar dan ligt het desbetreffende punt op de lijn lj, en is het dus het snijpunt van li en lj.
Bisectrices
Gegeven lijnen l2 en l3 kan je twee nieuwe lijnen, l2,3 en l2,3', construeren zodat de punten op l2,3 en 2,3' even ver van l2 als van l3 af liggen. Deze lijnen gaan door het snijpunt van l2 en l3, en delen alle hoeken tussen l2 en l3 doormidden. Ze worden wel bisectrices genoemd, 'bi' voor 'twee' en 'sectrice' van 'sectie', 'deel'.
Voor c op l2,3 geldt nu dat d2 = d3.
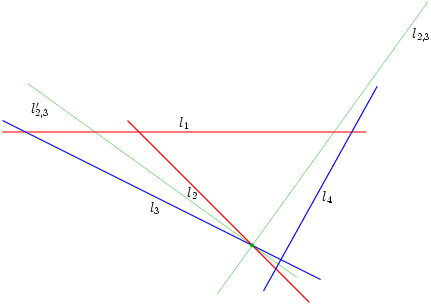
Op dezelfde manier kun je l1,4 en l1,4' construeren. Als je nu het snijpunt neemt van bijvoorbeeld l2,3 en l1,4 zie je dat in dit punt d2 = d3 en d1 = d4, dus d1×d2 = d3×d4. Dit geldt voor iedere combinatie van l1,4' of l1,4 en l2,3' of l2,3. In het plaatje hieronder stan drie van deze snijpunten (de vierde valt buiten het plaatje, maar bestaat wel).
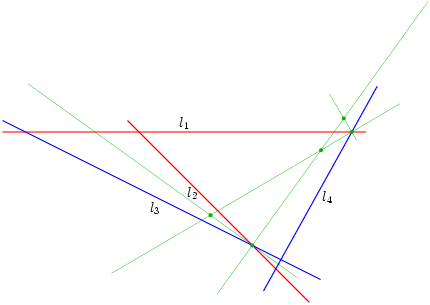
De bisectrices van l2 en l3 en l1 en l4 geven je al 4 punten. Je kunt natuurlijk ook de bisectrices van l1 en l3 snijden met die van l2 en l4, en dit geeft weer vier punten. Hieronder zie je een plaatje met bijna alle punten die je zo kunt vinden (er zijn er twee die erg ver weg liggen) De lijnen zijn weg gelaten om het geheel wat overzichtelijker te houden.
Merk op dat je er niets aan hebt om een bisectrice van l1 en l2 te snijden met een van l3 en l4: dan heb je immers een punt waar d1 = d2 en d3 = d4, maar dit zegt niet dat d1×d2 = d3×d4. Je kunt alleen bisectrices gebruiken tussen lijnen uit verschillende kanten van de vergelijking.
Merk ook op dat je weinig hebt aan deze methode als je vijf of meer punten hebt: je moet dan drie of meer bisectrices tekenen (omdat alle di gebruikt moeten worden), en het is niet zeker dat die drie lijnen elkaar in één punt snijden.
En nu?
We hebben nu een plaatje waar maar liefst acht punten van de oplossing in staan. We weten dat er nog twee zijn als we verder uitzoomen. Hoe ziet de hele oplossingsverzameling er uit?
Nu zie je duidelijk de beperkingen van klassieke passer-en-lineaal meetkunde: we kunnen wel losse punten vinden (als je je best doet kun je meer 'mooie lijnen' vinden, en daarmee nog meer punten construeren), maar als er oneindig veel oplossingen zijn (en dat is meestal zo) vinden we ze nooit allemaal. Toch willen we graag weten hoe de hele oplossingsverzameling er uit ziet, en hier komt Descartes om de hoek kijken.
Analytische meetkunde
Wat Descartes voorstelt is iets heel radicaals. Hij beschrijft punten als punten (x,y) in R2, en rechte lijnen als vergelijkingen van de vorm y = ax + b. Nu kan hij snijpunten van lijnen uitrekenen door de vergelijkingen aan elkaar gelijk te stellen, en hij kan makkelijk loodlijnen en bisectrices beschrijven in termen van de oorspronkelijke lijnen.
Hij kan ook de afstand di van een willekeurig punt (x,y) tot de lijn li beschrijven in termen van x en y. De vergelijking d1×d2 = d3×d4 wordt dan een (heel grote) vergelijking in x en y, en die kan je in principe gewoon uitwerken. Je krijgt dan een nieuwe vergelijking, die alle punten beschrijft die aan je eis dat d1×d2 = d3×d4 voldoen.
Waarom is dit zo radicaal? Het is toch logisch om een punt in het platte vlak te beschrijven met coördinaten, en rechte lijnen uit te drukken in x en y?
Dat is voor ons waar, maar je moet er maar op komen. Iemand moet als eerste bedenken dat dit kan en handig is, en dat was Descartes. Het is dan ook logisch dat hij moeite had zijn tijdgenoten te overtuigen: 'Meetkunde zonder passer of lineaal, en zonder constructies? Dat is toch helemaal geen meetkunde meer?'.
Voorbeeld van de methode van Descartes

In het plaatje hierboven zie je nog maar drie lijnen, die bovendien lekker makkelijk gekozen zijn: ze vormen een driehoek met hoeken van 45, 45 en 90 graden. Maar hoe kunnen we überhaubt aan de probleem van Pappus werken met maar 3 lijnen? Het antwoord is dat we vals gaan spelen: we tellen lijn 3 als lijn 3 en lijn 4. Dus l3 = l4, α3 = α4 en d3 = d4. De vergelijking wordt nu d1×d2 = d3×d4 = d32.
Om te beginnen gaan we ieder van de lijnen schrijven als een algebraische vergelijking in een x/y stelsel. We kunnen heel makkelijke vergelijkingen nemen door de assen goed te kiezen:
l1: y=0. (de x-as)
l2: x=0. (de y-as)
l3: y=1-x, of x+y=1.
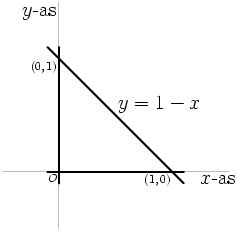
Hier zie de lijnen, met alle algebraische informatie er bij. Vergeet niet dat l3 = l4.
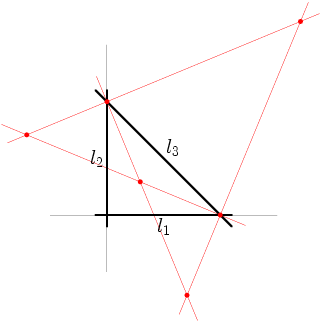
Hier zie je alle punten die kunnen vinden met de klassieke technieken die we hebben besproken.
We zullen nu laten zien hoe je voor een punt c de di berekent. Kies een punt c = (x,y) ergens in het platte vlak. Voor het gemak zullen we c zo kiezen dat x en y beiden positief zijn. Nu geldt dat d1 = de afstand van c tot de x-as = y. OP dezelfde manier: d2 = de afstand tot de y-as = x. Hoe berekenen we d3 (en daarmee d4)?
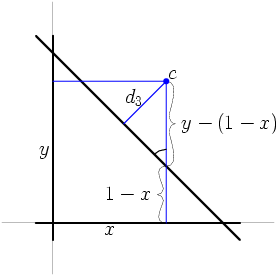
Je kunt zien dat de afstand van (x,y) tot l3 gelijk is aan de afstand van c tot l3 loodrecht naar beneden (het lijnstuk waar 'y-(1-x)' bij staat) maal de sinus van de hoek met het boogje. Omdat lijn l3 een hoek van 45 graden maakt met de x-as en de y-as is de hoek die we zoeken ook 45 graden.
De verticale afstand van punt c tot lijn l3 berekenen we als volgt: De hoogte van punt c is y. De hoogte van het punt op lijn l3 dat dezelfde x coördinaat heeft als c is 1-x. Het verschil tussen deze twee hoogten is wat we zoeken, en dit is y-(1-x). Het kan zijn dat dit negatief is (als c onder l3 ligt in plaats van erboven), dus nemen we de absolute waarde. Dus d3 = √(0.5) × absolute waarde(1-x-y) = √(0.5) × √((1-x-y)2).
We hebben nu alles uitgedrukt in x en y, en het ziet er tamelijk ingewikkeld uit. Het zal blijken dat als we alle invullen het best meevalt. We willen de volgende vergelijking oplossen:
d1 × d2 = d32.
Het invullen van alle gevonden di levert:
y × x = ( √(0.5) × √((1-x-y)2) )2.
We kunnen het buitenste kwadraat wegstrepen tegen de twee wortels:
xy = 0.5 × (1-x-y)2.
Het andere kwadraat uitwerken levert:
xy = 0.5 × ( x2 + y2 + 2xy - 2x - 2y + 1).
Alles naar een kant halen:
0.5 × (x2 + y2 + 1) - x - y = 0.
x2 + y2 - 2x - 2y + 1 = 0.
x2 + y2 - 2x - 2y + 2 = 1.
We kunnen nu te termen als volgt vergaren:
(x-1)2 + (y-1)2 = 1.
Die laatste vergelijking in de vergelijking van een cirkel met middelpunt (1,1) en straal 1.
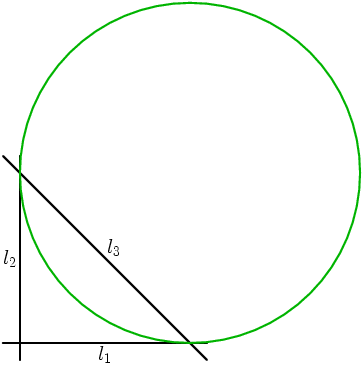
Hier zie je cirkel ingetekend in ons oorspronkelijke probleem
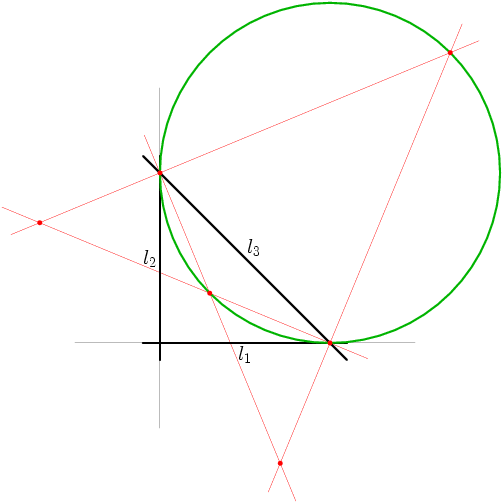
En hier zie je alle punten die we al hadden gevonden. Een aantal daarvan ligt keurig op de cirkel, maar een paar andere niet! Hoe kan dat?
Aan het begin van ons rekenwerk hebben we aangenomen dat x en y, de coördinaten van c, positief zijn. Als je nu bijvoorbeeld anneemt dat x of y negatief is, veranderen de formules om de afstanden d1, d2 en d3 te berekenen. Hierdoor wordt de vergelijking iets anders, en komt er (dit kan je zelf na gaan met wat rekenwerk) een hyperbool uit. Deze hyperbool bevind zich in de -x/+y en +x/-y kwadranten.
Samenvatting
Je hebt nu zelf kunnen zien hoe krachtig Descartes' 'nieuwe meetkunde' is: door je meetkundige probleem te beschrijven in algebraïsche termen kan je je oplossing berekenen, in plaats van construeren. Vaak (zoals bijvoorbeeld hierboven) kan je daarmee een probleem wel oplossen. Je hoeft bovendien geen creatieve oplossingen meer te verzinnen zoals in de klassieke meetkunde vaak nodig is, in plaats daarvan in het voldoende dat je je vergelijkingen juist opstelt, en zorgvuldig bent met plusjes en minnetjes.
Descartes' zelf claimt hiermee alle meetkundige problemen op te kunnen lossen. Dit is een duidelijk geval van overdrijving: als je bijvoorbeeld het probleem van Pappus neemt met 100 lijnen, heb je een vergelijking met 50 variabelen aan iedere kant. Hier komt een 50ste graads polynoom uit, en het oplossen daarvan of het omschrijven naar iets moois is alles behalve makkelijk.