Constructie van boogdeling, berekening van de koorde van de halve boog uit de koorde van de hele boog en het bewijs van de juistheid van de constructie
Constructie van boogdeling (zonder bewijs)
Gegeven: Een cirkel met middelpunt D en straal r
Twee punten A en B op die cirkel verbonden door lijnstuk AB.
We gaan het bijzondere punt E op boog AB construeren; later zal blijken dat dit het midden is van boog (AB)
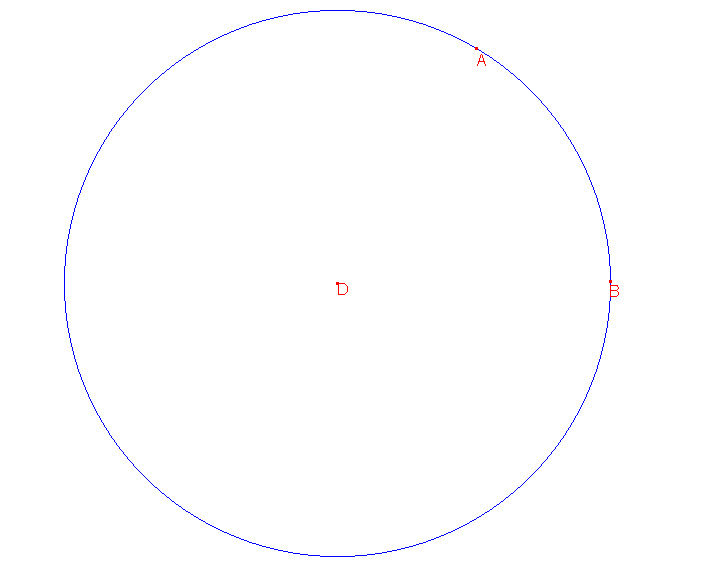
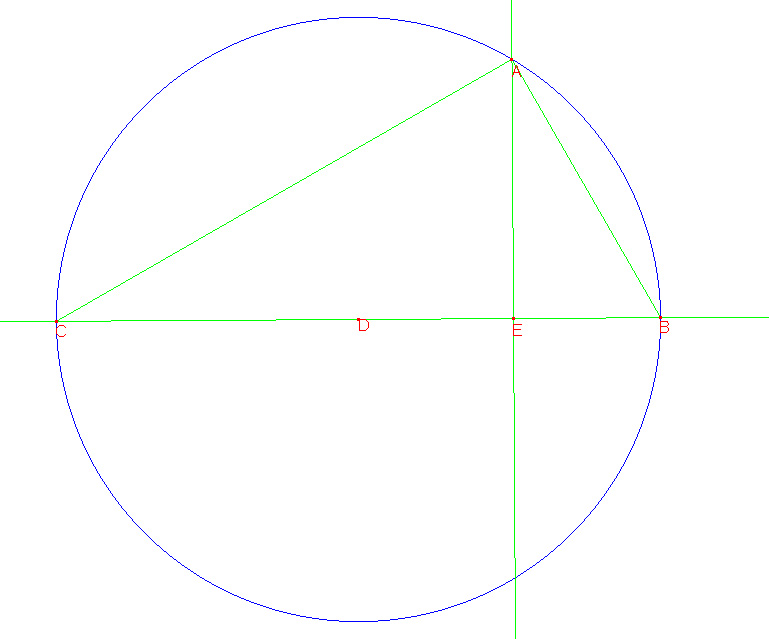
Teken de middellijn door B en D en laat het snijpunt van de middellijn en de cirkel C zijn
Teken vervolgens ook AC. Uit Euclides weten we dat hoek(BAC)=90°
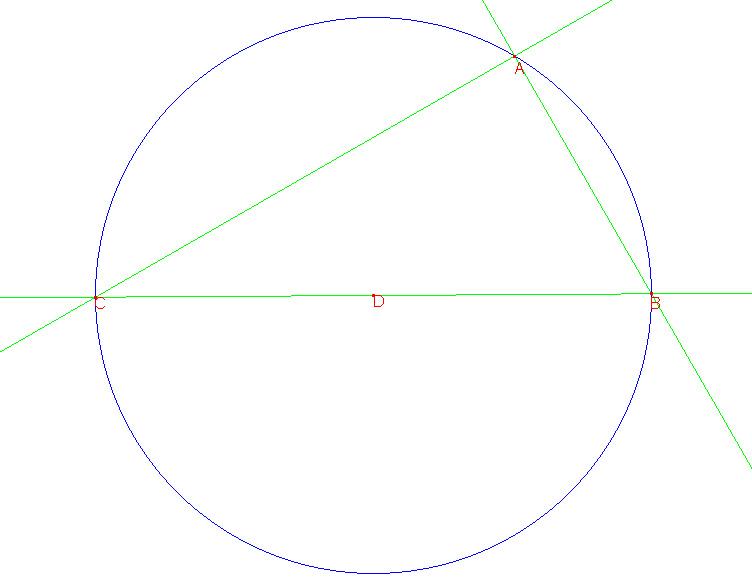
Construeer het punt x op BC zdd AC=CX
Construeer het punt s op BX zdd BS=SX
Construeer de loodlijn in S op BC en het laat snijpunt van deze loodlijn met de cirkel E zijn.
Teken ook BE
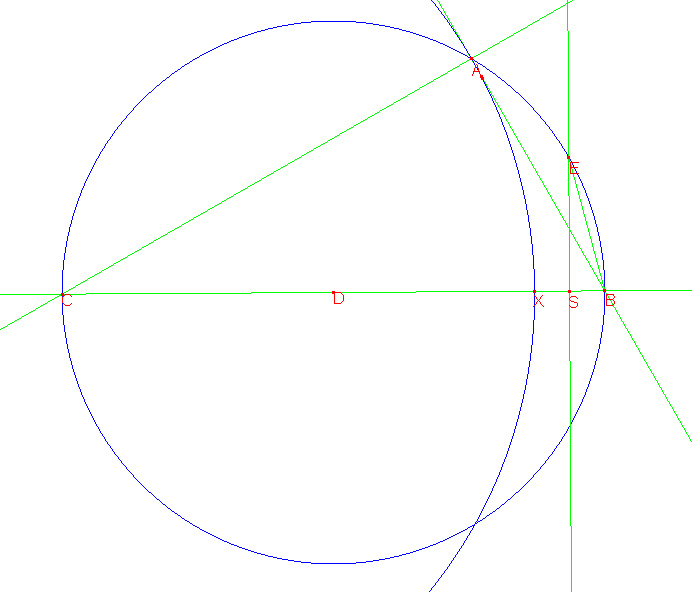
We hebben nu het punt E geconstrueerd.
Later zal bewezen worden dat E inderdaad het midden is van boog(AB), dus dat boog(AE)=boog(BE).
We gaan nu EB uitrekenen en dit gebeurt met niet-algebraïsche methoden omdat die nog niet beschikbaar waren.
Berekening van de koorde van de halve boog uit de koorde van de boog
Construeer het punt L op BD zó dat DL=BX en Z zó dat CZ=ZL
Teken nu de cirkel met middelpunt Z en straal ZL

Teken de loodlijn in D op BC en laat het snijpunt met de tweede cirkel H zijn.
Teken ook loodlijn op HD in H en een loodlijn in C op BC die elkaar snijden in M.

Construeer nu T op ES zdd BS=ST, dan de loodlijn in T die HD snijdt in R en de loodlijn op C in O en loodlijn B in P
Construeer ook punt Q op HD zdd DR=RQ en punt N op loodlijn C zdd CO=ON

Op plaatje 2 heb je nu een rechthoekige driehoek EBS, dus geldt dat EB2=ES2+SB2
omdat ST=SB en hoek(TSB)=90° geldt dat opp(STPB)=SB2
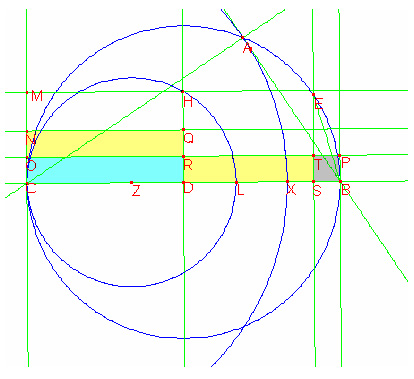
Van Euclides(prop 14 boek 2) weten we ook dat ES2=SB*CS en omdat SB=ST geldt ook dat ES2=opp(STOC)
Nu geldt dus dat EB2=ES2+SB2=opp(BPOC)=BP*BC=RD*BC=2RD*BC/2=opp(CNQD)
Weer uit Euclides(prop 14 boek 2) volgt dat HD2=CD*DL en omdat DL=QD geldt dat
EB2=HD2
We kunnen nu EB eenvoudig uitrekenen, immers:
De resultaten hierboven geven dat EB2=DL*CD en zowel DL als CD zijn eenvoudig te berekenen.
CD is namelijk de straal van de grote cirkel en DL is de diameter-AC;
En AC is dan weer makkelijk met de stelling van Pythagoras in driehoek ABC af te leiden omdat AB en BC bekend zijn.
Euclides: Propositie 14 boek 2
Gegeven:
Cirkel met middelpunt D en punten A en B op de cirkel.
C is het snijpunt van de lijn k door B en D met de cirkel.
Laat E het snijpunt van de loodlijn op BD door A
Dan geldt CE*BE=AE2
Bewijs van de juistheid van de contructie
In de eerste propositie construeerde van Ceulen dus het punt E (zie plaatje hieronder), dat volgens hem op het midden ligt van de boog AB, en berekende vervolgens de lengte van het lijnstuk EB in termen van het bekende lijnstuk AB. Maar hij bewees niet in zijn propositie dat het geconstrueerde punt E ook daadwerkelijk op het midden ligt van de boog AB. Aangezien ik niet weet hoe van Ceulen dit zou hebben bewezen zal ik hieronder een modern bewijs geven dat laat zien dat het geconstrueerde punt E ook daadwerkelijk op het midden van de boog AB ligt.
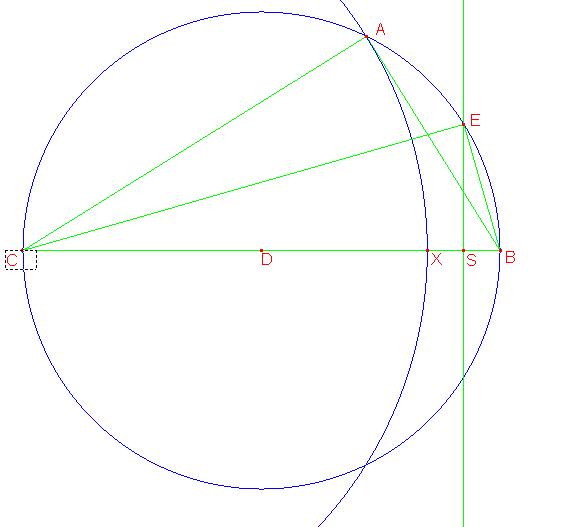
Gegeven:
• Een cirkel met middelpunt D en straal r
• De cirkel heeft diameter BC = 2r
• AB is een lijnstuk met uiteinden op de cirkel
Constructie van het punt E:
• X is het snijpunt van de cirkel met middelpunt C en straal AC met de diameter BC
• S is het midden van XB
• E is het snijpunt van de cirkel met de loodlijn door S op XB
Bewering:
E ligt op het midden van de boog AB
Bewijs:
In het bewijs van de eerste propositie bereikt van Ceulen het volgende resultaat voor de lengte van het geconstrueerde lijnstuk EB (in moderne notatie):
EB = √(2r2 - r AC)
Dit resultaat kunnen we dan gebruiken om verder te rekenen.
Aangezien driehoek EBC een rechthoekige driehoek is kunnen we EC bepalen met de stelling van pythagoras, namelijk:
EC2 = BC2 - EB2
Dus EC = √(4r2 - (2r2 - r AC)) = √(2r2 + r AC)
Nu bepalen we de sinus en cosinus van hoek ECB (vanaf nu in het kort α)
Sin(α) = EB / BC = EB / (2r)
Cos(α) = EC / BC = EC / (2r)
Vervolgens kunnen we Sin(2α) berekenen met behulp van de relatie:
Sin(2α) = 2Sin(α)Cos(α)
Toegepast op ons probleem geeft dit:
Sin(2α) = 2Sin(α)Cos(α) = 2(EBxEC) / (4r2) = {√[(2r)2 - (AC)2]} / (2r) = {√[(BC)2 - (AC)2]} / (2r)
Aangezien driehoek ABC ook een rechthoekige driehoek geldt dat (BC)2 - (AC)2 = (AB)2 dus:
Sin(2α) = 2Sin(α)Cos(α) = [√(AB2)] / (2r) = AB / (2r)
Als we nu de sinus van hoek ACB (vanaf nu in het kort β) berekenen dan zien we:
Sin(β) = AB / BC = AB / (2r) = Sin(2&aplha;)
Verder hebben we dat hoek β altijd tussen de 0 en 90 graden ligt dus kunnen we concluderen:
β = 2α
Gelijke hoeken geven gelijke bogen dus zien we:
Boog AB = 2 x Boog EB
Dus E ligt op het midden van boog AB