In het derde hoofdstuk beschrijft Van Ceulen hoe je met behulp van de propositie uit hoofdstuk 2 de zijden van een ingeschreven veelhoek kunt vinden, beginnende met de driehoek. In het vierde hoofdstuk doet Van Ceulen hetzelfde als in het derde hoofdstuk, maar nu begint hij met een vierhoek.

Hoofdstuk 3

Neem een cirkel met diameter 2 en de ingeschreven regelmatige driehoek ABC. De lengte van de zijde van de ingeschreven regelmatige zeshoek EB is gelijk aan de straal en is dus 1 (zie de 15e propositie van het 4e boek van Euclides). Zijn complement is BC, een zijde van de driehoek en heeft lengte √3. Dit laatste is gemakkelijk na te gaan met de stelling van Pythagoras: de zijde van de driehoek vormt samen met de zijde van de zeshoek en de diameter een rechthoekige driehoek EBC, zoals te zien is in het volgende plaatje:

Als we de lengte van het complement van EB aftrekken van de diameter houden we 2-√3 over. Dit is gelijk aan het kwadraat van de lengte van de zijde van de regelmatige ingeschreven twaalfhoek (zie hoofdstuk 2). Dus EF, een zijde van de twaalfhoek heeft lengte √(2-√3), wat gelijk is aan √(3/2)-√(1/2).

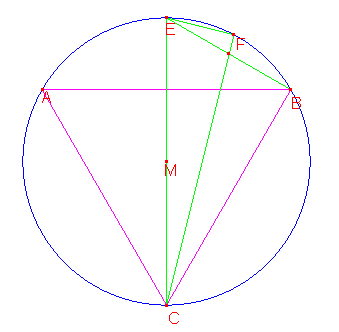
Met behulp van de stelling van Pythagoras zien we dat FC, het complement van EF, lengte √(2+√3) heeft (driehoek EFC is een rechthoekige driehoek). Als we dit aftrekken van de diameter krijgen we 2-√(2+√3). Dit is het kwadraat van de lengte van een zijde van de regelmatige ingeschreven 24hoek (zie weer hoofdstuk 2). Dus de lengte van zo'n zijde is √(2-√(2+√3)). Op dezelfde manier wordt gevonden dat de lengte van een zijde van de regelmatige ingeschreven 48hoek √(2-√(2+√(2+√3))), van de 96hoek √(2-√(2+√(2+√(2+√3)))) en van de 192hoek √(2-√(2+√(2+√(2+√(2+√3))))) is.

Hoofdstuk 4

Neem een cirkel met diameter 2 en de ingeschreven regelmatige vierhoek ABCD. De diagonalen BC en AD gaan door het middelpunt M en zijn dus gelijk aan de diameter. Er geldt dus BM = MD = 1. We weten dat hoek BMD een rechte hoek is. Uit de stelling van Pythagoras volgt nu: BD2 = BM2 + MD2 = 12 + 12 = 2. Omdat een lengte positief is, nemen we de positieve wortel en er geldt BD = √2. BD is een zijde van de vierhoek ABCD.

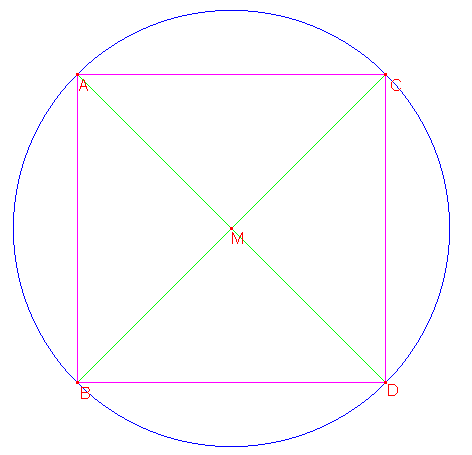
AB, ook een zijde van ABCD, is het complement van BD. Als we deze van de straal aftrekken, krijgen we 2-√2. Dit is het kwadraat van AE, een zijde van de regelmatige ingeschreven achthoek. Dus er geldt AE = √(2-√2).

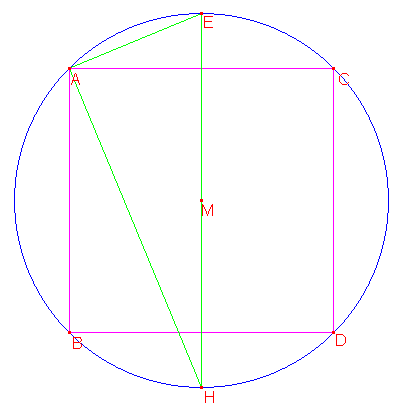
AH is het complement van AE. Hoek HAE is een rechte hoek, dus volgens de stelling van Pythagoras geldt: AH2 = EH2 - AE2 = 4 - (2 - √2) = 2 + √2. Dus AH = √(2+√2). Dit trekken we af van de diameter en zo krijgen we voor het kwadraat van de zijde van de regelmatige ingeschreven zestienhoek 2-√(2+√2). En er geldt dat EF, een zijde van de regelmatige ingeschreven zestienhoek, lengte √(2-√(2+√2)) heeft.

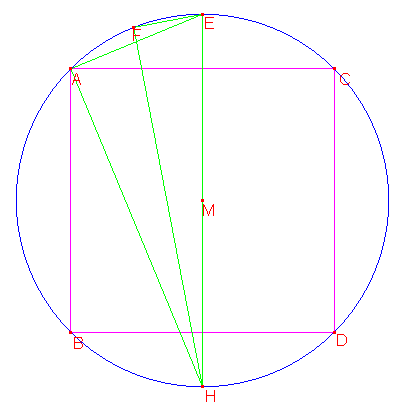
Op dezelfde manier wordt gevonden dat de lengte van een zijde van de regelmatige ingeschreven 32hoek √(2-√(2+√(2+√2))) en van de 64hoek √(2-√(2+√(2+√(2+√2)))) is.