In het vijfde hoofdstuk doet Van Ceulen hetzelfde als in het derde en het vierde hoofdstuk, maar nu begint hij met een vijf- en vijftienhoek.

Vijfhoek

In de proposities 11, 12, 13 en 14 van het vierde boek van Euclides wordt ons geleerd hoe we een regelmatige vijfhoek maken in of om een gegeven cirkel en een cirkel in of om een gegeven regelmatige vijfhoek. In de derde propositie van het veertiende boek van Euclides (het zogenoemde veertiende boek is geschreven door Hypsicles en door hem aan de dertien boeken van de Elementen van Euclides toegevoegd, overigens wordt hier de eerste propositie van dit boek bedoeld) staat hoe we een zijde van de regelmatige tienhoek vinden. Deze propositie zegt het volgende:
De loodrechte lijn van het middelpunt van een cirkel op een zijde van de ingeschreven regelmatige vijfhoek is de helft van de som van een zijde van de zeshoek en een zijde van de tienhoek, beide ingeschreven en regelmatig. Het bewijs gaat als volgt:

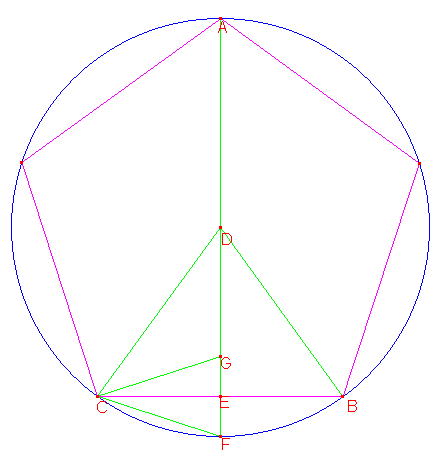
Neem een cirkel met middelpunt D en de ingeschreven regelmatige vijfhoek. BC is een zijde van die vijfhoek. Teken DE vanuit D loodrecht op BC en trek DE verder door zodat hij de cirkel snijdt in de punten A en F. Teken DC en CF en maak het punt G zodanig dat GE=EF en teken GC.
De boog van BFC is een vijfde van de hele cirkel en de boog van ACF is de helft van de hele cirkel. De boog van CF is de helft van de boog van BFC. Dus:

Boog van ACF = 5 * Boog van CF
Boog van AC = 4* Boog van CF

Dus er geldt:

Hoek ADC = 4 * Hoek CDF
Hoek AFC = 2 * Hoek CDF

Dus Hoek CGF = Hoek AFC = 2 * Hoek CDF
Er volgt nu dat Hoek CDG = Hoek DCG. (Hoek CGD + Hoek CGF = 180 graden; Hoek CDG + Hoek DCG + Hoek CGD = 180 graden, dus Hoek CDG = 180 - Hoek DCG - Hoek CGD = Hoek CGF - Hoek DCG = 2 * Hoek CDF - Hoek DCG = 2 * Hoek CDG - Hoek DCG, dus Hoek CDG = Hoek DCG).

Dus DG = GC = CF. Omdat GE = EF geldt nu DE = DG + GE = CF + EF. Als we aan beide kanten DE optellen, krijgen we 2DE = DF + CF en DF is een zijde van de ingeschreven regelmatige zeshoek (deze is gelijk aan de straal) en CF is een zijde van de ingeschreven regelmatige tienhoek.

Om de lengte van een zijde van de ingeschreven regelmatige tienhoek te berekenen, maken we gebruik van een andere constructie.

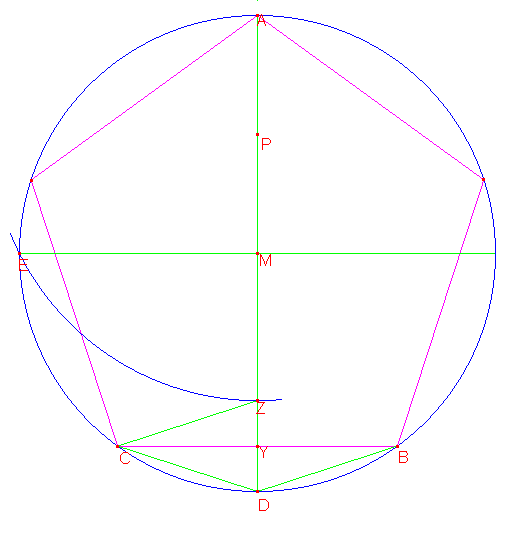
Neem een cirkel met middelpunt M en de ingeschreven regelmatige vijfhoek. Het punt P ligt op de helft van de straal, dus AP=PM. We tekenen de cirkelboog met middelpunt P en straal EP. Het snijpunt hiervan met de lijn AD noemen we Z. We zullen aantonen dat Z gelijk is aan het punt G in de eerste tekening.

Stel dat we Z hetzelfde definiëren als punt G (dus niet als het snijpunt van de cirkelboog met de lijn AD, maar als ZY=YD). Dan geldt MZ=ZC=CD. Omdat de driehoeken MDC en CDZ gelijkvormig zijn (zelfde hoeken), hebben we de volgende verhoudingen MD:MZ = MD:DC = CD:DZ = MZ:DZ. Dit houdt in dat het vierkant met zijde MZ gelijk is aan de rechthoek met zijden MD en DZ.

Analoog aan het punt P definiëren we punt Q op de helft van MD, dus MQ=QD.
Er geldt PZ2 = (PM + PZ)2 = (QM + MZ)2 = QM2 + 2QM*MZ + MZ2
Aangezien QM = PM, 2QM = MD en MZ2 = MD*DZ, krijgen we:
PZ2 = PM2 + MD*MZ + MD*DZ = PM2 + MD*MD = PM2 + MD2 = PM2 + ME2 = PE2.

Dus punt Z ligt op de cirkel met middelpunt P en straal PE. Dus MZ is een zijde van de ingeschreven regelmatige tienhoek en de lengte hiervan vinden we als volgt:

MP2=1/4
EM=1
Dus volgens de stelling van Pythagoras geldt EP2=1 1/4
Dus PZ = EP = √(1 1/4)
Nu volgt voor CD, een zijde van de tienhoek: CD = MZ = PZ - MP = √(1 1/4) - 1/2

Voor BC, een zijde van de ingeschreven regelmatige vijfhoek, kunnen we als volgt de lengte uitrekenen. Het complement van CD is AC. Volgens de stelling van Pythagoras geldt dat AC2=22 - (√(1 1/4) - 1/2)2 = 2 1/2 + √(1 1/4)
Dus AC=√(2 1/2 + √(1 1/4)).

Er geldt CD * AC = BC, dus BC =√(2 1/2 - √(1 1/4))

Met behulp van de propositie uit Hoofdstuk 2 kunnen we nu de lengtes van de zijden van de ingeschreven regelmatige 20-,40- en 80hoek vinden. De zijde van de 20hoek heeft lengte √(2 - √(2 1/2 + √(1 1/4))), van de 40hoek √(2 - √(2 + √(2 1/2 + √(1 1/4)))) en van de 80hoek √(2 - √(2 + √(2 + √(2 1/2 + √(1 1/4))))). En zo kunnen we verder gaan met veelvouden van 20.

Vijftienhoek

Een zijde van de ingeschreven regelmatige vijftienhoek kunnen we als volgt construeren:

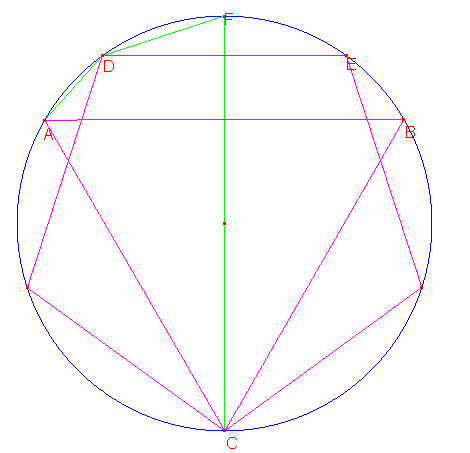
Neem een cirkel met straal 1 en de ingeschreven regelmatige drie- en vijfhoek. AB is een zijde van de driehoek, DE van de vijfhoek en DF van de tienhoek.
De boog van BEFDA is dus een derde van de hele cirkel. De boog van FDA is hier de helft van en dus een zesde deel van de hele cirkel. De boog van FD is een tiende van de hele cirkel. Hieruit volgt dat de boog van DA een vijftiende van de hele cirkel is (1/6 - 1/10 = 1/15). Dus DA is een zijde van de vijftienhoek.

De lengte van AD kunnen we als volgt berekenen:

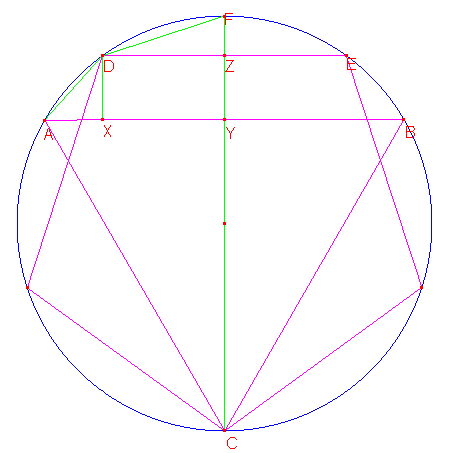
We tekenen een lijnstuk vanuit D loodrecht op DE (en dus ook loodrecht op AB) en het snijpunt met AB noemen we X.
AX = 1/2 zijde driehoek - 1/2 zijde vijfhoek
FZ2 = (zijde tienhoek)2 - (1/2 zijde vijfhoek)2
FY = 1/2
FY - FZ = ZY = DX
AD2 = AX2 + DX2

Als we de getallen die we in hoofdstuk 3,4 en 5 hebben gevonden invullen krijgen we: AD = √(5/8+√(5/64)) - √(9/8-√(45/64)).

Met behulp van de propositie uit Hoofdstuk 2 kunnen we de lengtes van zijden van veelhoeken met een veelvoud van 15 aan hoeken uitrekenen. Voor de lengte van de zijde van de ingeschreven regelmatige 30hoek vinden we bijvoorbeeld √(2 1/4 - √(5/16) -√(15/8 +√(45-64))).