wiskonst.nl

In het korte achtste hoofdstuk laat Van Ceulen zien hoe je, uitgaande van de zijde van een ingeschreven veelhoek, de inhoud van deze veelhoek te berekenen.

De methode die Van Ceulen gebruikt om de oppervlakte te berekenen is door het werk dat hij reeds gedaan heeft nogal eenvoudig. Een regelmatige n-hoek bestaat immers uit n gelijkbenige driehoeken, dus het is voldoende een van die driehoeken te berekenen en die oppervlakte weer met n te vermenigvuldigen. Bij het betreffende hoofdstuk stond het figuur hier direct onder, maar omdat er veel in dat figuur staat dat je niet nodig hebt om de methode te begrijpen gebruik ik voor de methode het figuur dat bij aanname 20 hoort. In dat figuur wil ik de oppervlakte van driehoek ABD berekenen en dat is 1/2*AB*ED. We gaan uiteraard uit van n een veelvoud van 3, 4 en/of 5, dus hij kan met zijn methode AB uitrekenen. Verder volgt uit de 20e aanname dat ED gelijk is aan de helft van CB en deze CB is eenvoudig uit te rekenen met de stelling van Pythagoras, aangezien AB en AC bekend zijn en ABC een rechthoekige driehoek is.

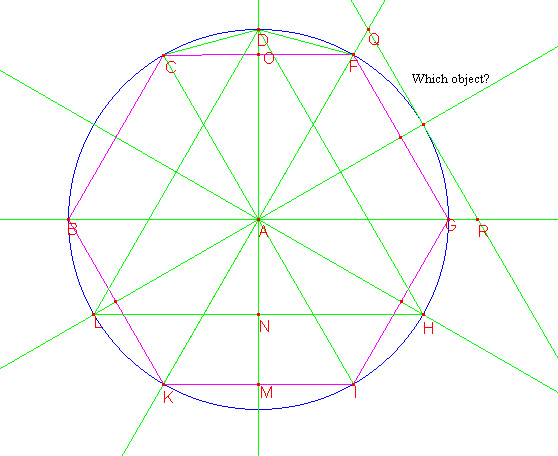
Van Ceulen geeft een groot aantal voorbeelden, waarvcan ik er hier een paar zal geven. Hierbij gebruik ik het figuur hier direct boven.

Voorbeeld 1:
Hij begint met de oppervlakte van de gelijkzijdige driehoek DLH. De zijden van die driehoek zijn √(3). NH is de helft daarvan, 1/2*√(3)=√(3/4). Berekenen we vervolgens in rechthoekige driehoek DNH de zijde DN door √(DH2-NH2)=√(3-3/4)=3/2. De oppervlakte van DLH (in het boek staat DBH, maar dit klopt niet. Dus ik vermoed dat het gewoon een drukfout is) is dan 3/2*√(3/4)=√(27/16).

Voorbeeld 1:
Vervolgens bekijkt hij de gelijkzijdige zeshoek CFGIKB. Hij gaat nu de oppervlakte van de driehoek AIK berekenen. Eerst merkt hij op dat de zijde van de zeshoek gelijk is aan de straal van de cirkel, hier 1. Dan zegt hij dat uit de 20e aanname volgt dat AM gelijk is aan √(3/4) en dit is eenvoudig in te zien, aangezien KI de zijde van een regelmatige zeshoek is en het complement daarvan de zijde van een regelmatige driehoek is. Dus AM=1/2*CK=√(3/4). En de oppervlakte van de regelmatige zeshoek wordt dan 3*KI*AM=3*AM=√(27/4).

Na deze voorbeelden zegt Van Ceulen dat het echter nog veel makkelijker kan, en hier verwijst hij naar Euclides. Stel dat je de inhoud van een ingeschreven zeshoek wilt berekenen. Deze inhoud is precies gelijk aan de zijde van de driehoek maal 3/2. Volgens de zelfde methode is de inhoud van de 12-hoek gelijk aan de zijde van de zeshoek maal 3. Deze methode gebruikt Van Ceulen om de inhoud van een aantal ingeschreven veelhoeken te berekenen. De resultaten van deze berekeningen zijn verder niet zo interessant, aangezien we die nu zeer gemakkelijk uit kunnen rekenen.