In het negende hoofdstuk laat Van Ceulen zien hoe je, gegeven de lengte van de zijde van een ingeschreven veelhoek, de lengte van de zijde van een omgeschreven veelhoek met even veel hoeken kunt berekenen. Vervolgens gebruikt hij dit resultaat om een methode voor de kwadratuur van de cirkel als fout te bestempelen.

Berekening

In de vorige hoofdstuk heeft Van Ceulen laten zien hoe je vrij makkelijk de lengte van de zijden van (sommige) ingeschreven veelhoeken kunt berekenen. Gegeven deze lengte, en een cirkel met straal 1, kun je vrij simpel de lengte van de zijde van een omgeschreven veelhoek berekenen. Dit gaat als volgt: trek een lijn loodrecht op de ingeschreven zijde door het middelpunt van de cirkel. Deel de lengte van de ingeschreven zijde nu door de lengte van het lijnstuk dat tussen deze zijde en het middelpunt van de cirkel loopt. Het resultaat is de lengte van de zijde van de omgeschreven veelhoek. Dit wordt door Van Ceulen als volgt aangetoond:

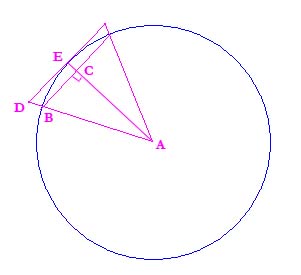
We gebruiken de gelijkvormigheid van driehoek ABC en driehoek ADE. Door gelijkvormigheid hebben corresponderende zijden dezelfde verhouding. Driehoek ADE staat tot driehoek ABC als AE staat tot AC. AE heeft lengte 1, want is gelijk aan de straal van de cirkel. De verhouding tussen ABC en ADE is dus 1:lengte AC. Dus om DE te berekenen kunnen we BC delen door de lengte van AC. Dus 2 maal DE is gelijk aan 2 maal BC gedeeld door AC. Dit levert precies op wat Van Ceulen beweert in hoofdstuk 9. Met dit resultaat gaat Van Ceulen verder werken. Eerst beschrijft hij 2 methode om de kwadratuur van de cirkel te bepalen, die van Carolus Bovillus en A. Barbel. Uitgaande van een cirkel met diameter 1, komen beide methodes tot een omtrek van wortel 10. Van Ceulen laat nu gemakkelijk zien dat dit niet kan kloppen, door met behulp van de in- en omgeschreven 30-hoek een onder- en bovengrens voor deze omtrek te vinden (die overigens pi moet zijn). Als hij vervolgens de wortel van 10 uitrekent komt hij tot de conclusie dat dit resultaat groter is dan de bovengrens voor de omtrek die hij net berekend heeft. Hiermee laat hij dus zien dat zowel Barbel als Bovillus fouten gemaakt hebben in hun methoden.