Derde deel des eersten boucx van het teyckenen der lichamen

Stevin zegt van plan te zijn alleen het teyckenen van lichamen (d.w.z. driedimensionale figuren) te behandelen voorzover daarvoor wetenschappelijke kennis nodig is. Hij gaat niet in op de willekeurige bouwsels die "int wilde na der wercklieden inval gheformt worden". Uit de inhoud van de proposities die volgen blijkt dat Stevin met het woord teyckenen niet persé tekenen bedoelt. Alleen in propositie 17 legt hij uit hoe je een bepaalde figuur (de balk) op papier construeert, maar voor de rest houdt hij zich bezig met het bouwen van echte driedimensionale objecten, bijvoorbeeld van hout of karton.

Voorstel 17: Een plattich lichaem van begheerde form te teyckenen.
In deze propositie legt Stevin uit hoe men een plattich lichaem (een veelvlak, een lichaam opgebouwd uit vlakken) maakt van een gewenste afmeting, als er een veelvlak van dezelfde vorm (maar andere grootte) gegeven is. Zoals gebruikelijk geeft hij geen algemene methode, maar beperkt hij zich tot een voorbeeld: het verkleinen van een gegeven balk ABCDEFG.

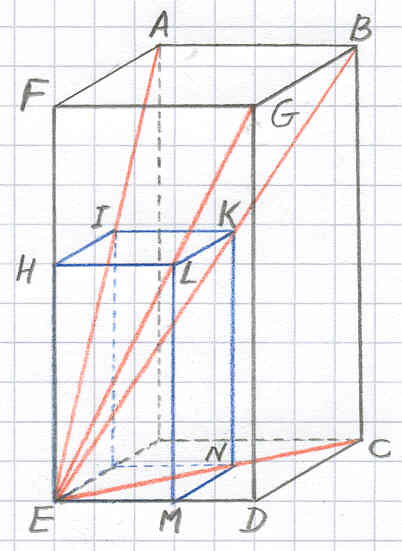De bedoeling is, een van de ribben (EF) te verkorten (tot EH) en vanuit de korte ribbe een nieuwe balk te tekenen die gelijkvormig is met de oude. Dit doet Stevin door eerst het hoekpunt E met alle andere hoekpunten van de balk te verbinden (voorzover die verbindingslijnen er nog niet waren): trek de lijnen EA, EB, EC en EG. Vervolgens tekent hij vanuit het punt H een nieuwe balk, waarvan de ribben evenwijdig lopen aan de ribben van de oude balk, en waarvan de hoekpunten op de eerder getrokken diagonalen uit E liggen. Deze nieuwe balk voldoet.
Stevin bewijst niet dat de gevonden balk IKNMEHL inderdaad gelijkvormig is met ABCDEFG, en geeft zelfs geen verwijzing naar zo'n bewijs.

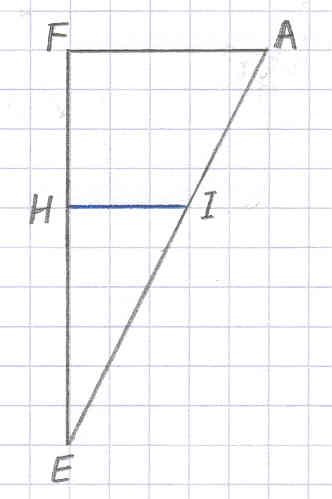Het eerste nieuwe hoekpunt dat Stevin construeert bij het tekenen van de nieuwe balk is het punt I (de punten E en H lagen al op de oude balk). Daarbij ontstaat de figuur hiernaast. Omdat HI parallel getrokken is aan FA, zijn de driehoeken EFA en EHI gelijkvormig. Daarom geldt:
(*) HI : EH = FA : EF
Het volgende punt dat Stevin construeert is het punt L, en geheel analoog volgt uit deze constructie dat
(**) EH : HL = EF : FG

Het bewijs dat IKNMEHL gelijkvormig is met ABCDEFG volgt nu als speciaal geval van propositie 27 van boek 11 van de Elementen van Euclides:
[Euclid 1956, III, p. 329] On a given straight line to describe a parallelepipedal solid similar and similarly situated to a given parallelepipedal solid.
Een balk is een speciaal soort parallellepipedum, net zoals een rechthoek een speciaal soort parallellogram is, dus we mogen de constructie die Euclides in zijn bewijs geeft hier toepassen. Dat bewijs is na te lezen in [Euclid 1956], maar juist omdat een balk een speciaal parallellepipedum is, mogen we een aantal stappen overslaan. Het blijkt voldoende te zijn om vanaf de ribbe EH de punten I en L zo te kiezen dat (*) en (**) gelden. Vanuit de punten E, H, I en L is de balk uniek bepaald: de rest van de constructie is een kwestie van (evenwijdige) lijntjes trekken. Euclides' propositie 27 van boek 11 zegt nu dat de gevonden balk IKNMEHL inderdaad gelijkvormig is met ABCDEFG.

Stevin schrijft vervolgens dat deze methode voornamelijk van theoretisch belang is, dat wil zeggen bij het tekenen van figuren op papier. In de praktijk, wanneer we te maken hebben met echte, tastbare voorwerpen, bestaat er volgens hem een eenvoudiger manier van werken. (In dat geval kan men de lijn EB in de bovenstaande figuur niet trekken, want deze loopt door het lichaam heen. Uit het bewijs via Euclides bleek al dat de constructie ook werkt als deze lijn wordt weggelaten.) Als voorbeeld uit de praktijk noemt Stevin het in het klein namaken van een gebouw.

Stel dat men de (echte) balk ABCDEFG wil nabouwen, uitgaande van een gegeven ribbe EH, net zoals in het getekende voorbeeld hierboven. Na het meten van de ribben van de balk (N.B. Stevin heeft nog niet behandeld hoe zo'n meting verricht moet worden; dat komt pas in het tweede boek ter sprake.) blijkt dat EF 8 voeten lang is en FG 4 voeten. (Deze getallen zijn natuurlijk willekeurig, maar Stevin werkt graag met concrete voorbeelden.) Stevin voert nu een nieuwe maat in, de "kleine voet", die hij zo kiest dat EH 8 kleine voeten lang is. Hij maakt de ribbe HL (die de rol van FG overneemt) 4 kleine voeten lang, en in het algemeen zorgt hij ervoor dat een ribbe in de oude balk die x voeten meet, overeenkomt met een ribbe in de nieuwe balk die x kleine voeten meet. Met behulp van een winkelhaak is uit deze losse ribben een balk te maken. Deze balk IKNMEHL is gelijkvormig met de oude balk ABCDEFG, omdat de verhoudingen tussen de ribben onderling niet veranderd zijn: alleen de maat is anders.

Stevin schrijft verder nog dat de beschreven methodes voor elk plattich lichaem gebruikt kunnen worden. Omdat bij ingewikkeldere figuren niet elke hoek negentig graden is, heeft men daarbij in de praktijk behalve een winkelhaak ook een instrument nodig dat andere hoeken aan kan geven. Timmerlieden gebruiken daarvoor volgens Stevin de Leughenswee, een soort grote passer zonder punt, waarmee men hoeken kan afpassen.

Voorstel 18: De vijf gheschickte lichamen te teyckenen.
Een gheschickt lichaem heet tegenwoordig een regelmatig veelvlak (ook wel: Platonisch lichaam, naar Plato), net zoals een gheschickt plat een regelmatige veelhoek is. Stevin noemt een lichaam een gheschickt lichaem als het "t'eenemael omvanghen in ghelijcke ende even gheschickte platten" is. Zijn woordkeuze is voor ons wat verwarrend: met ghelijck bedoelt Stevin gelijkvormig en met even bedoelt hij gelijk, d.w.z. even groot. Een gheschickt lichaem - of een regelmatig veelvlak - is dus een lichaam dat is opgebouwd uit identieke regelmatige veelhoeken.
Strikt genomen hoort hier nog de voorwaarde bij dat het veelvlak gesloten en convex is, maar Stevin lijkt dit stilzwijgend aan te nemen: alle lichamen die in de Meetdaet voorkomen zijn gesloten en convex.

Er bestaan precies vijf regelmatige veelvlakken, zoals Stevin opmerkt. Euclides bewijst dit aan het slot van zijn Elementen, in het vervolg op propositie 18 van boek 13:
[Euclid 1956, III, p. 507] No other figure, besides the said five figures, can be constructed which is contained by equilateral and equiangular figures equal to one another.

Hieronder staan de vijf regelmatige veelvlakken afgebeeld. (Deze plaatjes zijn gemaakt met het computerprogramma Maple.)

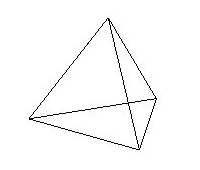De tetraëder, of het regelmatig viervlak: een piramide van gelijkzijdige driehoeken.

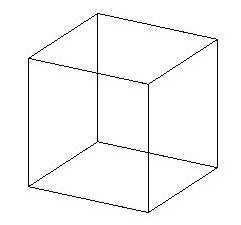De hexaëder, of het regelmatig zesvlak, meestal kubus genoemd.

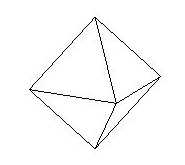De octaëder, of het regelmatig achtvlak: twee piramides met een vierkant grondvlak tegen elkaar geplakt.

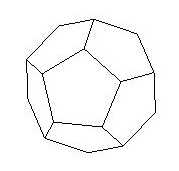De dodecaëder, of het regelmatig twaalfvlak, opgebouwd uit regelmatige vijfhoeken.

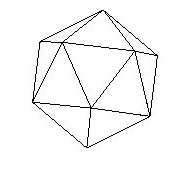De icosaëder, of het regelmatig twintigvlak, opgebouwd uit gelijkzijdige driehoeken.

Dit zijn de enige vijf volledig regelmatige veelvlakken. Wel is het volgens Stevin mogelijk een regelmatig veelvlak te snijden zodat een figuur ontstaat die in veel opzichten lijkt op een regelmatig veelvlak (maar het niet is). Die half-regelmatige veelvlakken bezitten namelijk een aantal eigenschappen die regelmatige veelvlakken ook hebben:

Omdat echter niet alle vlakken van zo'n gesneden regelmatig veelvlak hetzelfde zijn, kan men niet spreken van een regelmatig veelvlak. In propositie 19 buigt Stevin zich nader over deze half-regelmatige veelvlakken.

Stevin geeft van elk regelmatig veelvlak een plattegrond. Deze plattegronden kan men namaken van bijvoorbeeld ghepapt papier of plat coper, en dan vouwen tot de gewenste figuur. Als men liever een veelvlak bouwt van vollijveghe stof (hout, bijvoorbeeld), kan men daarvoor gebruik maken van de praktische methode uit propositie 17.

Voorstel 19: De gheschickte ghesneen lichamen te teyckenen.
In deze propositie geeft Stevin plattegronden voor een aantal half-regelmatige veelvlakken, net zoals hij dat in propositie 18 met de regelmatige veelvlakken deed. De theorie van de half-regelmatige veelvlakken was in de tijd van Stevin nog grotendeels onontgonnen terrein: de enige voorloper die hij had was Albrecht Dürer, die in zijn boek Unterweysung der Rechnung mit dem Zirckel und Richtscheyt (1525) zeven van deze veelvlakken beschreef. Stevin nam de door Dürer ontdekte veelvlakken over in zijn Problemata Geometrica (1583) en voegde er zelf drie aan toe. Hij was waarschijnlijk de eerste zestiende-eeuwer die tien half-regelmatige veelvlakken kende.

Maar kort na het verschijnen van de Problemata Geometrica werd Stevins ontdekking alweer achterhaald: in 1588 verscheen een Latijnse vertaling van het verzameld werk van Pappus (ca. 300 na Chr.), met daarin een beschrijving van dertien half-regelmatige veelvlakken, ontleend aan een - niet teruggevonden - werk van Archimedes (ca. 250 voor Chr.). Deze kennis uit de klassieke Oudheid was in de Middeleeuwen verloren gegaan. Hoewel de Meetdaet pas zo'n twintig jaar later werd uitgegeven, heeft Stevin de nieuwe informatie niet gebruikt. (In tegendeel zelfs, de Meetdaet bevat juist twee half-regelmatige veelvlakken minder dan de Problemata Geometrica!) Waarschijnlijk heeft hij het werk van Pappus niet gelezen.

De door Archimedes gevonden dertien zijn in feite alle half-regelmatige veelvlakken die er bestaan. Men noemt ze daarom ook wel Archimedische veelvlakken. Een handige notatie voor het beschrijven van veelvlakken, gebruikt in [Stevin 1958], is de volgende: een veelvlak bestaande uit m regelmatige a-hoeken, n regelmatige b-hoeken, etc. wordt opgeschreven als {m_a, n_b, ...}. Een tetraëder, die immers bestaat uit vier gelijkzijdige driehoeken, wordt dus genoteerd als {4₃}, en {12₅} is een dodecaëder.

In de volgende tabel staan de dertien Archimedische veelvlakken in deze notatie, met daarbij aangegeven welke Dürer kende en welke Stevin beschreef in de Problemata Geometrica en in de Meetdaet:

	naam	Dürer	Stevin 1583	Stevin 1605
{43, 46}	afgeknotte tetraëder	*	*	*
{83, 64}	cubo-octaëder	*	*	*
{64, 86}	afgeknotte octaëder	*	*	*
{83, 68}	afgeknotte kubus	*	*	*
{83, 184}	romben-cubo-octaëder	*	*	*
{124, 86, 68}	grote romben-cubo-octaëder	*	*	*
{203, 125}	icosi-dodecaëder		*	*
{125, 206}	afgeknotte icosaëder		*
{203, 1210}	afgeknotte dodecaëder		*
{203, 304, 125}	romben-icosi-dodecaëder
{304, 206, 1210}	grote romben-icosi-dodecaëder
{323, 64}	stompe kubus	*	*	*
{803, 125}	stompe dodecaëder

De plattegronden die Stevin in propositie 19 geeft zijn dus te vouwen tot, in volgorde: de afgeknotte tetraëder, de afgeknotte kubus, de cubo-octaëder, de stompe kubus, de romben-cubo-octaëder, de grote romben-cubo-octaëder, de afgeknotte octaëder en de icosi-dodecaëder.

Meer informatie over Stevin en half-regelmatige veelvlakken is te vinden in de inleiding op de Problemata Geometrica in [Stevin 1958]. Een redelijk toegankelijke wiskundige beschrijving van allerlei veelvlakken (regelmatig, half-regelmatig en nog andere soorten) is te vinden in [Vegt 1991]. In beide boeken staan ook afbeeldingen van alle dertien Archimedische veelvlakken.

Voorstel 20: Den cloot te teyckenen.
In deze propositie bedoelt Stevin met teyckenen duidelijk geen tekenen: er komt geen papier of potlood in voor. In plaats daarvan geeft hij twee methoden uit de praktijk om een bol te maken, bijvoorbeeld van hout. (Cloot is Stevins woord voor bol.) Van beide methoden geeft hij niet meer dan een algemene beschrijving.

De eerste methode is die van de draeybanck. Deze is vooral geschikt voor het maken van kleine bollen. Men neemt een stuk hout dat al enigszins de juiste vorm heeft, zet dit vast in de draaibank met de pinnen op twee tegenoverelkaar gelegen punten, en draait het hout rond in de bank totdat een cirkel met de juiste diameter is ontstaan. Daarna zet men het hout op twee andere punten vast en draait men een cirkel in de nieuwe richting. Eventueel herhaalt men het procédé nogmaals met twee nieuwe punten. Uiteindelijk ontstaat volgens Stevin op deze manier een bol. Hij geeft echter geen manier om te bepalen wanneer het stuk hout precies bolvormig geslepen is. Waarschijnlijk bepaalde de bolmaker dit met het blote oog.

Voor grotere bollen gebruikt men volgens Stevin een halfronde mal in plaats van een draaibank. Over deze tweede methode is hij nog korter van stof: "een halfronde malle, (...) alwaermen over al vervult datter int halfrondt ghebreeckt, of wegh neemt datter te veel is". Ook hier geeft hij geen methode om te zien wanneer de bol 'af' is. Hij gaat niet in op de vraag hoe de halfronde mal - immers ook een bolvormig voorwerp - gemaakt is. Misschien op de draaibank?

Tenslotte merkt Stevin nog op dat mallen ook gebruikt kunnen worden voor het maken van clootschen (sferoïden, omwentelingsellipsoïden), keghels en keghelschen (omwentelingsparaboloïden). Natuurlijk kun je op deze manier elke figuur maken die je wilt, als je maar de juiste mal gebruikt.