Eerste deel des tweeden boucx vant meten der linien

Stevin behandelt achtereenvolgens drie methoden voor het meten van lijnen: door overgheleyde mate (meten in de moderne zin des woords, met liniaal e.d.), door sichtstralen (m.b.v. instrumenten) en door ander bystaende bekende linien (door gebruik te maken van stellingen uit de meetkunde).

Voorstel 1: Een rechte lini door overgheleyde maet te meten.
Bij metingen op kleine schaal - in het bijzonder bij metingen op papier - maakt men volgens Stevin gebruik van een leer, een soort liniaal. Het woord leer betekent eigenlijk ladder. Stevin legt omstandig uit hoe men zo'n liniaal gebruikt aan de hand van een voorbeeld, waarin hij de zijden van een driehoek opmeet.

Stevin gebruikt de gelegenheid om reclame te maken voor de decimale breuken, zoals hij ze in De Thiende (1585) heeft ingevoerd. Prins Maurits is volgens hem een enthousiast gebruiker van deze notatie: "(...) waer deur sijn Vorstelicke Ghenade verscheyden metinghen der grootheden, als de naervolghende sijn, met soo groot gherief, lichticheyt ende sekerheyt ghedaen heeft, dat de proeven van dien haer gheen cleene vernoughing en gaven."

Bij metingen op grotere schaal kan men beter gebruik maken van ketens, aldus Stevin. Hij laat een tekening zien van zo'n keten, die bestaat uit een aantal roeden die in elkaar gehaakt zitten. De roeden zijn meestal gemaakt van ijzerdraad of koperdraad, en niet van touw, want dat kan uitgerekt worden. Elke roede heeft een schaalverdeling, doorgaans in twaalf voeten, die weer bestaan uit twaalf duimen. Stevins roede heeft - daar is De Thiende weer - ook een schaalverdeling in tienden en honderdsten.

Bij het meten van de afstand tussen twee punten A en B met een keten, moet men te voet van A naar B lopen. Soms is dit niet mogelijk (obstakels in het landschap) of wenselijk (te grote afstand). Stevin noemt dergelijke afstanden ongherakelicke langden of onghenakelicke langden. In dat geval kan men gebruik maken van de volgende methode: het meten door sichtstralen. Er bestaan hiervoor verschillende instrumenten (wisconsttuyghen), die in grote lijnen echter hetzelfde werken. Stevin bespreekt daarom slechts één zo'n instrument: de drieroe.

De drieroe bestaat uit drie roeden: een dikke grondroe, een rechterroe en een (s)lin(c)kerroe. De rechter- en de linkerroe kunnen beide gedraaid worden. Bij de rechterroe, die op een vast punt op de grondroe zit, is een gradenboog gemonteerd om de hoek te meten die hij met de grondroe maakt. De linkerroe kan over de grondroe verschoven worden en op elk punt worden vastgezet. Alledrie de roeden zijn voorzien van een schaalverdeling en van sichtpinnen. Als grondstof is messing (lattoen) het meest geschikt.

Voorstel 2: Deur sichtstralen onghenakelicke sichteindersche langden te meten.
In Voorbeeld I legt Stevin duidelijk uit hoe een meting met de drieroe in zijn werk gaat. In de praktijk blijkt de drieroe eenvoudig in het gebruik. De enige wiskunde die men erbij nodig heeft bestaat uit gelijkvormigheid van driehoeken en rekenen met verhoudingen: in het voorbeeld zijn de driehoeken CEF en CBA gelijkvormig, dus er geldt: EC : EF = BC : BA. Omdat van deze vier afstanden alleen AB onbekend is, kan deze nu snel gevonden worden.

In Voorbeeld II laat Stevin Prins Maurits opmerken dat men de afstand ook kan meten zonder gebruik te maken van de schaalverdeling op de roeden. Dit vereist wel iets meer wiskunde. Hij verwijst hiervoor naar "het 4 voorstel der platte driehoucken". Het boek Vande platte driehoucken is een onderdeel van het boek Vanden driehouckhandel, dat op zijn beurt weer een onderdeel is van het Weereltschrift, het eerste deel van de Wisconstighe Ghedachtenissen, waartoe ook de Meetdaet behoort. In de vierde propositie van het boek van de vlakke driehoeken legt Stevin uit hoe men in een driehoek waarvan twee hoeken en een zijde bekend zijn, de derde hoek en de andere twee zijden berekent. De derde hoek vindt men eenvoudig door toe te passen dat de som van de hoeken 180° moet zijn. Voor het vinden van de twee onbekende zijden gebruikt Stevin de eerste propositie van hetzelfde boek, die zegt:
Ghelijck des platten driehoucx rechtersijde totte slinckersijde, alsoo slinckerhoucx houckmaet, tot rechterhoucx houckmaet.

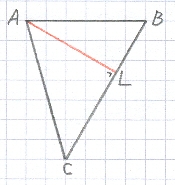
De houckmaet van een hoek is (min of meer) wat tegenwoordig de sinus heet. Stevins propositie zegt dus dat in de hiernaast getekende driehoek ABC geldt dat:
(*) AB : AC = sin C : sin B.
Modern gezien volgt dit direct uit de definitie van de sinus:
sin C = AD : AC en sin B = AD : AB,
en bij het delen vallen de twee AD's tegen elkaar weg.
(Stevins bewijs is iets langer, omdat de definitie van de hoekmaat niet precies gelijk is aan die van de moderne sinus.)

Het is met deze propositie inderdaad mogelijk om, zoals Prins Maurits opmerkte, de afstand AB te bepalen als alleen de hoeken bij B en C en de afstand BC bekend zijn. De hoek bij A is dan ook bekend: hoek A = 180° – hoek B – hoek C. Uit de bovenstaande propositie volgt (hernoem de hoeken op de juiste wijze):
BC : AB = sin A : sin C
en van deze vier getallen is alleen AB onbekend.

Stevin laat vervolgens zien dat het ook mogelijk is de afstand te bepalen zonder hoeken te meten. Dit vereist echter meer meetwerk en lijkt dan ook alleen bedoeld voor situaties waarbij geen drieroe beschikbaar is.

In Voorbeeld III laat Stevin zien hoe de drieroe gebruikt wordt bij het meten van een afstand AB waarbij noch A noch B bezocht wordt. De werking is in grote lijnen hetzelfde en wederom wordt de afstand berekend uit verhoudingen in gelijkvormige driehoeken. In het bewijs dat de driehoeken ICK en ACB gelijkvormig zijn staat een drukfout: "Want IC sulcken reden heeft tot KC, als AC tot AB" moet zijn "Want IC sulcken reden heeft tot KC, als AC tot BC". (Zie Stevins tekst voor de bijbehorende figuur.)

Net als in voorbeeld II is het ook mogelijk de afstand AB te vinden door slechts twee zijden (AC en BC) en een hoek (de hoek bij C) te meten. Stevin doet dit in de zesde propositie van het boek Vande platte driehoucken met behulp van sinus (houckmaet) en tangens (raecklijn).
Eerst vindt men AL dankzij: sin C = AL : AC.
Vervolgens bepaald men LC uit: tan C = AL : LC.
BL volgt nu eenvoudig: BL = BC – LC.
Nu geldt: tan B = AL : BL, en hiermee vinden we de hoek B. (Bij een daadwerkelijke berekening zouden wij de functie tan^-1 of arctan op de rekenmachine gebruiken. In Stevins tijd gebruikte men hiervoor tabellen met benaderingen.)

De gevraagde zijde AB vinden we nu volgens: sin B = AL : AB.

(De bovenstaande berekening volgt Stevins aanpak. Het bewijs gaat (iets) korter door de stelling van Pythagoras toe te passen. Bij een daadwerkelijke berekening moet men dan natuurlijk worteltrekken, wat in Stevins tijd (zonder rekenmachine!) een nogal tijdrovend werk was. Logisch dus dat Stevin liever gebruik maakte van sinus en tangens, waarvoor hij tabellen beschikbaar had.)

Voorstel 3: Deur sichtstralen ongherakelicke hooghde en diepte te meten.
In Voorbeeld I gebruikt Stevin de drieroe voor het bepalen van een hoogte, loodrecht op de grond. De werking is min of meer hetzelfde als in de tweede propositie, alleen wordt nu de grondroe verticaal opgesteld (evenwijdig aan de te meten hoogte). In het plaatje dat Stevin erbij geeft is een van de mogelijke toepassingen te zien: het opmeten van een kerktoren.

In de eerste opmerking behandelt Stevin een situatie waarin men niet in de volledige hoogte geïnteresseerd is, maar alleen wil weten hoe ver deze boven het eigen standpunt uitkomt. Hierin staat een drukfout: "Soomen wilde weten hoe veel t'punt B hoogher is dan t'punt A" moet zijn "Soomen wilde weten hoe veel t'punt B hoogher is dan t'punt E". In de tweede opmerking volgt het meten van de diepte onder het eigen standpunt.

In de derde opmerking behandelt Stevin de (niet denkbeeldige) situatie dat men de afstand tot de te meten hoogte niet kan bepalen - een gegeven dat voor de in voorbeeld I behandelde methode vereist is. Men kan nog steeds de drieroe gebruiken, maar nu zijn twee metingen op twee standen nodig.

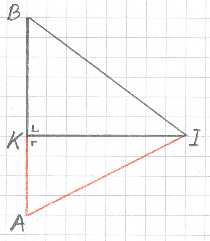In Voorbeeld II laat Stevin wederom zien dat de hoogte ook met minder gegevens gevonden kan worden. Hij gaat terug naar de situatie uit de eerste opmerking bij voorbeeld I en meet nu alleen de afstand IK en de hoek BIK. Hieruit kan de gevraagde afstand KB gevonden worden met behulp van de eerder genoemde vierde propositie uit het boek Vande platte driehoucken.
De hoek BKI is namelijk 90°, dus per definitie geldt:
tan BIK = KB : IK,
en hierin is de hoogte KB de enige onbekende.
Met dezelfde aanpak is ook de diepte KA uit de tweede opmerking te vinden. KB en KA zijn samen de totale hoogte AB, die dus eveneens op deze manier bepaald kan worden.

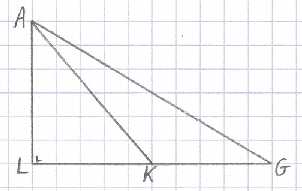Vervolgens behandelt Stevin de situatie uit de derde opmerking op dezelfde manier. De te meten hoeken zijn hier AGK en AKG, en de enige gemeten afstand is GK, de afstand tussen de twee standplaatsen. (In de praktijk wordt de hoek AKL gemeten, waaruit hoek AKG volgt omdat die twee samen 180° maken.)
Door de betrekking (*) toe te passen op de driehoek AKG, kunnen we de zijde AK bepalen uit: AK : GK = sin KGA : sin KAG, waarbij de hoek KAG gelijk is aan 180° min de hoeken AGK en AKG.

Vervolgens bekijken we de driehoek AKL. Hiervan is de zijde AK nu bekend, en verder kennen we de hoek AKL en de hoek ALK, die 90° is. Er geldt per definitie: sin AKL = AL : AK, en hieruit volgt de gevraagde hoogte AL.
(Stevin verwijst in de laatste regel van dit voorbeeld naar "het 3 voorstel der platte driehoucken". Dit lijkt ons een drukfout, want die propositie zegt alleen dat de hoeken van een driehoek samen 180° zijn. Een verwijzing naar de vierde propositie ligt meer voor de hand.)

In Voorbeeld III behandelt Stevin een methode uit Holland voor het bepalen van de hoogte van dijken. Hij gebruikt hier een drieroe, maar geeft toe dat een simpeler instrument (bijvoorbeeld een waterpas) in feite net zo goed werkt. In Voorbeeld IV tenslotte, laat hij zien dat de tot nu toe gehanteerde beperking, dat de te meten hoogte loodrecht op de grond staat, niet nodig is. Ook scheefhouckiche hoogtes zijn met de drieroe te bepalen.

Voorstel 4: Deur des driehoucx drie bekende sijden, te vinden de twee hanghendensgronden ende hanghende.
Een hanghende is een loodlijn (Engels: perpendicular).
In deze propositie maakt Stevin gebruik van twee proposities uit de Elementen van Euclides. In Voorbeeld I verwijst hij naar propositie 13 van boek 2:

[Euclid 1956, I, p. 406] In acute-angled triangles the square on the side subtending the acute angle is less than the squares on the sides containing the acute angle by twice the rectangle contained by one of the sides about the acute angle, namely that on which the perpendicular falls, and the straight line cut off within by the perpendicular towards the acute angle.
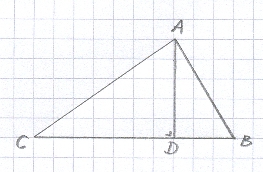
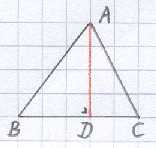
Dat wil zeggen, in de driehoek ABC hiernaast geldt:
AC² = AB² + BC² – 2·BC·BD.

Bewijs: Volgens Euclides' eerdere propositie 7 van boek 2 geldt:
BC² + BD² = 2·BC·BD + DC².
(Dit is het meetkundige equivalent van: a² + b² = 2ab + (a – b)², met a = BC en b = BD.)
Dus geldt ook:
BC² + BD² + AD² = 2·BC·BD + DC² + AD².
Vanwege de stelling van Pythagoras geldt: AB² = BD² + AD², en AC² = DC² + AD², dus:
BC² + AB² = 2·BC·BD + AC².
Breng 2·BC·BD naar de andere kant en de relatie is bewezen. [QED]

Stevins berekening bestaat nu uit het simpelweg invullen van alle bekende grootheden in Euclides' betrekking:
AC² = AB² + BC² – 2·BC·BD,
waaruit de onbekende BD gevonden wordt, en vervolgens CD en de loodlijn AD.

In Voorbeeld II behandelt hij een driehoek met een stompe hoek, waarbij de loodlijn buiten de driehoek valt. Hiervoor past hij Euclides' propositie 12 van boek 2 toe:

[Euclid 1956, I, pp. 403-404] In obtuse-angled triangles the square on the side subtending the obtuse angle is greater than the squares on the sides containing the obtuse angle by twice the rectangle contained by one of the sides about the obtuse angle, namely that on which the perpendicular falls, and the straight line cut off outside by the perpendicular towards the obtuse angle.
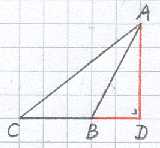
Dat wil zeggen, in de driehoek ABC hiernaast geldt:
AC² = AB² + BC² + 2·BC·BD.

Bewijs: Volgens Euclides' eerdere propositie 4 van boek 2 geldt:
CD² = BC² + BD² + 2·BC·BD.
(Dit is het meetkundige equivalent van: (a + b)² = a² + b² + 2ab, met a = BC en b = BD.)
Dus geldt ook:
CD² + AD² = BC² + BD² + AD² + 2·BC·BD.
Vanwege de stelling van Pythagoras geldt: AC² = AD² + CD², en AB² = BD² + AD², dus:
AC² = BC² + AB² + 2·BC·BD. [QED]

Stevins berekening bestaat nu uit het simpelweg invullen van alle bekende grootheden in Euclides' betrekking:
AC² = AB² + BC² + 2·BC·BD,
waaruit de onbekende BD gevonden wordt, en vervolgens CD en de loodlijn AD.

Voorstel 5: Wesende bekent de vijf linien vallende int meten der verheyt van twee punten deur twee standen: Te vinden deur ghetalen de langde tusschen de twee metelicke punten.
In deze propositie past Stevin de resultaten van de vorige propositie toe.
Onder Tbereytsel staat een drukfout: "Laet ghetrocken worden AB" moet zijn "Laet ghetrocken worden AG".

Voorstel 6: Wesende ghegheven een bijl met vier bekende sijden: Haer hanghende van d'een der evewijdeghe op d'ander te vinden.
In deze propositie geeft Stevin nog een toepassing van de vierde propositie: het vinden van de loodlijn in een bijl, dat wil zeggen een trapezium.

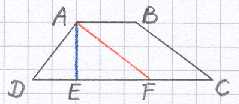De aanpak is zeer rechttoe rechtaan. Stevin heeft alle informatie van de propositie en de drie vervolgen die erbij horen in één plaatje gestopt. Omdat de tekening daardoor wat onduidelijk is geworden, hebben we het voor Twerck relevante gedeelte hiernaast nog eens getekend.

Voorstel 7: Bekent wesende de sijde eens gheschickt plats: Te vinden de lini vant middelpunt tot een houck.
Het houckmaetmaecksel waarnaar Stevin in de inleiding van deze propositie verwijst is het boek Vant maecksel des tafels der Houckmaten, het eerste deel van Vanden driehouckhandel. (Het eerdergenoemde Vande platte driehoucken is het tweede deel.)

Stevin laat in deze propositie zien - bij wijze van getallenvoorbeeld - hoe men de afstand bepaalt tussen het middelpunt en een hoekpunt van een regelmatige zevenhoek, waarvan de lengte van de zijde bekend is. Deze afstand is de straal van de omgeschreven cirkel om de zevenhoek. (Een gheschickt plat is een regelmatige veelhoek.)

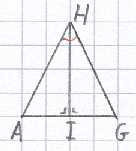Hiernaast staat een deel van de figuur uit de Meetdaet. AG is een zijde van de regelmatige zevenhoek ABCDEFG en heeft lengte 6; H is het middelpunt. HI is de middelloodlijn op AG. Gevraagd is dus de lengte van AH.
Per definitie geldt: sin AHI = AI : AH.
Dus: 2·sin AHI = 2·AI : AH = AG : AH,
en daarom geldt: AH = AG : (2·sin AHI).

Stevin gebruikt in zijn berekening weer de houckmaet, de voorloper van de sinus. Voor de duidelijkheid volgt hier de berekening in moderne notatie:

Stevins uitkomst AH = 60000000 : 8677676 = 6 ^7933944/_8677676 = 6,9142936... wijkt hier nauwelijks van af.

In het tweede vervolgh staat een drukfout: "des rechthouckighen driehoucx HI" moet zijn "des rechthouckighen driehoucx HIA". De schilboochs houckmaet die hierin genoemd wordt is de voorloper van de cosinus.

Voorstel 8: Deur de bekende middellijn des rondts den omtreck te vinden.
Een propositie over wat wij het getal pi noemen. In Stevins tijd werd de verhouding tussen de omtrek en de middellijn van een cirkel echter nog niet genoteerd als de Griekse letter pi. Die notatie stamt pas uit de achttiende eeuw.

Stevin noemt een aantal benaderingen die op dat moment bekend waren:

De benadering van Van Ceulen was op dat moment (1605) de beste, maar Stevin maakt er in de Meetdaet geen gebruik van. Om de berekeningen simpel te houden stelt hij vanaf nu: pi = ²²/₇. Het gelijkteken moet men hier letterlijk nemen: in de rest van de Meetdaet doet Stevin alsof pi exact ²²/₇ is, en niet bij benadering.

Hij schrijft bijvoorbeeld: "7 gheeft 22, wat AC 12 ? comt voor den begheerden omtreck 37 ⁵/₇. T'bewijs daer af is ghedaen int bouck vande meting des rondts van Archimedes." Strikt genomen is dat niet waar: Archimedes bewijst in Over de cirkelmeting alleen dat de omtrek van deze cirkel niet groter is dan 37 ⁵/₇. (En niet kleiner dan 37 ⁴⁹/₇₁.)

Stevin schrijft: "(...) de reden der middellijn totten omtreck [en is] als noch niet volcommelick ghevonden (...)". Hij hield dus de mogelijkheid open dat later de verhouding tussen de omtrek en middellijn van een cirkel alsnog exact bekend zou worden. Dat is niet gebeurd: in 1767 bewees Lambert dat pi niet als breuk van gehele getallen geschreven kan worden (pi is irrationaal), en in 1882 bewees Lindemann dat pi zelfs transcendent is: er bestaat geen polynoomvergelijking met gehele coëfficiënten die pi als oplossing heeft.

Voorstel 9: Wesende bekent eens boochs peez ende haer rondts halfmiddellijn: Dien booch te vinden.
Het woord peez betekent koorde, dat wil zeggen een recht lijnstuk dat twee punten op een kromme (in dit geval een cirkel) verbindt.

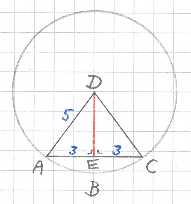Stevins berekening is iets makkelijker te noteren door het middelpunt van AC ook een naam te geven: noem dit punt E.
Er geldt: sin ADE = AE : AD = (½·AC) : AD.
Omdat AC en AD bekend zijn, is hiermee de hoek ADE te vinden. (Modern: sin^-1 op de rekenmachine. In Stevins tijd: hoekmaattabellen.)
De hoek ADC is dubbel zo groot, en dit is tevens de hoek die de boog ABC opspant. De lengte van de boog is nu gelijk aan: omtrek hele cirkel × (hoek ADC : 360°)

Voorstel 10: Wesende bekent de drie sijden eens driehoucx: Te vinden de middellijn haers omschrijvelick rondts.
Er is een driehoek ABC gegeven waarvan alle zijden een bekende lengte hebben. De driehoek heeft een omgeschreven cirkel, en de lengte van de middellijn AD van deze cirkel moet gevonden worden.
Twerck van deze propositie begint met (opnieuw) een toepassing van de vierde propositie: Stevin bepaalt de loodlijn AE op de zijde BC. (Merk op: de hier gebruikte driehoek is precies gelijk aan die uit het voorbeeld in de vierde propositie.)

De nieuwe driehoek ABE is gelijkvormig met ADC, de driehoek die een van de zijden van ABC en de middellijn van de cirkel bevat. Daaruit volgt: AE : AB = AC : AD. En, zoals Stevin opmerkt, trouwens ook: AE : AC = AB : AD. Uit beide uitdrukkingen is AD onmiddellijk te bepalen, want de lengtes van de zijden AB en AC zijn bekend.

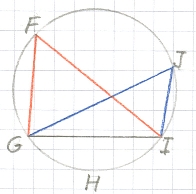Voor het bewijs dat de driehoeken ABE en ADC gelijkvormig zijn maakt Stevin gebruik van de 21ste propositie van het 3e boek van de Elementen van Euclides:

[Euclid 1956, II, p. 49] In a circle the angles in the same segment are equal to one another.

Dat wil zeggen, in de cirkel FGHIJ hiernaast zijn de hoeken GFI en GJI gelijk, omdat ze beide de koorde GI opspannen.
In Stevins figuur betekent dit dat de hoeken ABC en ADC gelijk zijn.

In Stevins figuur is de hoek ACD 90°, omdat deze hoek wordt gevormd door twee lijnen (AC en CD) die samen precies de middellijn AD opspannen. Dit is geen triviale opmerking. Euclides bewijst het in propositie 31 van boek 3 van de Elementen, [Euclid 1956, II, pp. 61-65].

Omdat de hoeken ABC en ADC gelijk zijn, en de hoeken ACD en AEB allebei 90°, zijn de driehoeken ABE en ADC inderdaad gelijkvormig.