Derde deel des vyfden boucx vande everedelicke snyding der lichamen

Voorstel 16: Van een ghegheven rechtlinighe pylaer een begheert deel te snyen na een getoonden oirt, met een plat evewijdich vanden as, diens plats ende des gronts ghemeene sne evewijdeghe sy van een ghestelde lini.

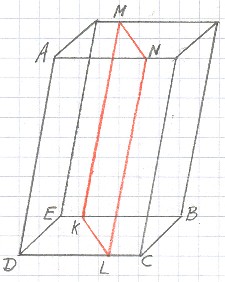In deze propositie behandelt Stevin de volgende opgave: gegeven zijn een prisma AB, met grondvlak BCDE, en twee lijnstukken F en GH, waarvan GH gesneden is in het punt I. Verdeel het prisma nu in twee stukken, KLDE en KLCB, door het in de hoogte te snijden, waarbij het snijvlak KLNM evenwijdig loopt met het gegeven lijnstuk F (dat wil zeggen: de snijlijn KL van dit vlak met het grondvlak van het prisma moet evenwijdig lopen met F). Voor de inhoud van de twee stukken moet gelden:
Inhoud(KLDE) : Inhoud(KLCB) = GI : IH.

In propositie 14 van dit boek heeft Stevin al laten zien hoe men het grondvlak BCDE middels een snijlijn KL in twee stukken KLDE en KLCB verdeeld zodat geldt:
Oppervlakte(KLDE) : Oppervlakte(KLCB) = GI : IH.
Volgens Stevin is deze lijn KL tevens de snijlijn van het gezochte snijvlak KLNM met het grondvlak. Het vlak KLNM is dan eenvoudig te tekenen: de lijnstukken KM en LN lopen evenwijdig aan DA, een staande ribbe van het prisma.

Het bewijs hiervoor is simpel. De twee deelprisma's KLDE en KLCB zijn zelf ook prisma's, met dezelfde hoogte als het hele prisma bovendien, en voor de inhouden geldt dus:
Inhoud(KLDE) = Oppervlakte(KLDE) × h,
Inhoud(KLCB) = Oppervlakte(KLCB) × h,
waarbij h de hoogte van het oorspronkelijke prisma AB is.
De verhouding tussen de inhouden van de twee deelprisma's is daarom gelijk aan de verhouding van hun grondvlakken, en die verhouding is precies GI : IH.

Voorstel 17: Van een ghegheven pylaer een begheert deel te snyen na een ghetoonden oirt, met een plat evewijdich vanden gront.
Deze propositie vormt een natuurlijk vervolg op de vorige: ditmaal moeten we een gegeven prisma ABCD in horizontale richting in tweeën snijden, met een snijvlak evenwijdig aan het grondvlak van het prisma, zodat voor de twee delen HIBA en HICD geldt:
Inhoud(HIBA) : Inhoud(HICD) = EG : GF,
waarbij EF een gegeven lijnstuk is dat in G gesneden is.

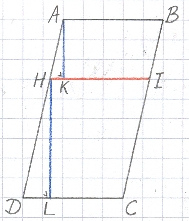Wederom zijn de twee delen HIBA en HICD zelf weer prisma's, en wel prisma's met hetzelfde grondvlak (nl. het vlak door HI). Daarom geldt:
Inhoud(HIBA) : Inhoud(HICD) = hoogte(HIBA) : hoogte(HICD).
Die hoogtes zijn in het plaatje hiernaast aangegeven met AK en HL, respectievelijk.
Hoewel de hoogtes niet gegeven zijn, kunnen we wel iets zeggen over hun verhouding:
AK : HL = AH : HD.
Immers, AK = AH · sin AHK en HL = HD · sin HDL, en de hoeken AHK en HDL zijn gelijk.

Stevin snijdt daarom de staande ribbe AD in tweeën bij het punt H, zodat AH : HD = EG : GF, en tekent vervolgens door H het snijvlak evenwijdig aan het grondvlak van het prisma.

Voorstel 18: Van een ghegheven rechtlinighe naelde een begheert deel te snyen na een ghetoonden oirt, met een t'plat deur t'soppunt diens ende des gronts ghemeene sne evewijdeghe sy van een ghestelde lini.
Dit is het analogon van de 16e propositie voor piramides. Stevins methode werkt precies hetzelfde als bij prisma's. Het bewijs gaat ook hetzelfde, omdat de inhoud van een piramide gelijk is aan een derde van de inhoud van het prisma met hetzelfde grondvlak en dezelfde hoogte, en omdat bij het doorsnijden van de piramide twee kleinere piramides ontstaan.

Voorstel 19: Van een ghegheven naelde een begheert deel te snyen na een ghetoonden oirt, met een plat evewijdich vanden gront.
Dit is het analogon van de 17e propositie voor piramides, maar in tegenstelling tot de vorige propositie kunnen we hier niet dezelfde methode gebruiken als bij prisma's. Bij het horizontaal doorsnijden van een piramide ontstaan namelijk niet twee deelpiramides, maar een piramide en een afgeknotte piramide.

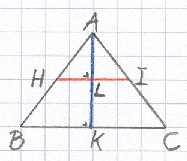Van de piramide ABC, waarvan hiernaast een doorsnede is getekend, moet een kleinere piramide AHI worden afgesneden (waarbij het grondvlak HI van de kleine piramide evenwijdig loopt aan het grondvlak BC van de grote).
Het punt H moet hierbij zo gekozen worden, dat de verhouding tussen de inhoud van AHI en die van de afgeknotte piramide HICB een voorgeschreven waarde heeft:
Inhoud(AHI) : Inhoud(HICB) = DF : FE,
waarbij DE een gegeven lijnstuk is dat gesneden is in het punt F.

Stevins methode werkt als volgt:

De inhoud van de piramide ABC is evenredig met de derdemacht van de hoogte AK:
Inhoud(ABC) = k × AK³,
waarbij k een constante van evenredigheid is. De piramides AHI en ABC zijn gelijkvormig, en daarom is de inhoud van AHI evenredig met de derdemacht van de hoogte AL volgens dezelfde evenredigheidsconstante:
Inhoud(AHI) = k × AL³.
Voor de verhouding geldt daarom:
Inhoud(AHI) : Inhoud(ABC) = ( AL : AK )³.
Zoals we in propositie 17 hebben gezien, geldt er:
AL : AK = AH : AB,
en omdat AH = ABx, volgt er:
(*) Inhoud(AHI) : Inhoud(ABC) = x³ = DF : DE.

Vervolgens maakt Stevin gebruik van iets dat hij ghescheyden reden noemt. Het scheyden van een reden betekent dat uit de bewering:
a : b = c : d
volgt dat ook geldt:
a : (b – a) = c : (d – c).
(Mits b > a.)
Uit (*) concludeert Stevin daarom dat:
Inhoud(AHI) : (Inhoud(ABC) – Inhoud(AHI)) = DF : (DE – DF),
en omdat de afgeknotte HICB ontstaat door de piramide AHI uit de piramide ABC weg te halen, staat daar:
Inhoud(AHI) : Inhoud(HICB) = DF : FE,
zoals gevraagd was.

N.B. Het begin van Stevins bewijs verloopt iets anders dan hier. Hij stelt dat uit de constructie van G en AH volgt dat G de vierde evenredige is van AB en AH, d.w.z.:
AB : AH = AH : G₁ = G₁ : G.
Dit is inderdaad zo:
AH : AB = x, dus G₁ = AHx = ABx², en G = G₁x = ABx³ = AB × ^DF/_DE.

De rest van Stevins bewijs is boven al behandeld.

Stevin geeft nog een duidelijk getallenvoorbeeld, en Prins Maurits heeft (weer) een andere aanpak gevonden:
AB : AH = ¹/_x,

dus:
AB³ : AH ³ = ¹/_x³ = DE : DF,

waaruit de lengte van AH direct berekend kan worden, omdat de lengtes van de andere lijnstukken bekend zijn. Deze aanpak gaat echter in tegen de regels van de klassieke (Griekse) meetkunde, omdat het lijnstuk AH niet geconstrueerd wordt. Voor praktische berekeningen maakt Stevin er toch gebruik van.

In de eerste zin van Tbereytsel staat overigens een drukfout: "Laet ghetrocken worden den hanghende van A op de gront B" moet zijn "Laet ghetrocken worden den hanghende van A op de gront BC".

Voorstel 20: Van een ghegheven cloot een begheerde halfmiddellijnsne te snyen.
Stevin introduceerde de halfmiddellijnsne in propositie 25 van boek 2. Een moderne vertaling is "bolsector".

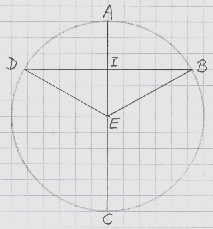In de tweedimensionale tekening hiernaast is EDAB een bolsector. Hij wordt geconstrueerd door twee tegenoverelkaar gelegen punten D en B op gelijke hoogte op de bolrand, te kiezen en die met het middelpunt E van de bol te verbinden. Het punt I ligt op de middellijn AC en geeft aan hoe hoog D en B liggen. Uit het plaatje is duidelijk dat de bolsector uniek bepaald is door dit punt I.
(Strikt genomen is EDCB, het stuk bol dat achterblijft, ook een bolsector. We kunnen de inhoud van EDCB echter eenvoudig afleiden als we de inhoud van EDAB en van de hele bol ABCD kennen. Daarom kunnen we voor het gemak aannemen dat de bolsector EDAB altijd kleiner is dan de helft van de bol.)

In drie dimensies is duidelijker te zien dat de bolsector in feite bestaat uit twee delen: een boltop (het cirkelsegment DBA uit de tekening hierboven om zijn eigen as gewenteld) en een kegel (de driehoek DBE om zijn eigen as gewenteld).
(Dit plaatje is gemaakt met het computerprogramma Maple.)

De opgave in deze propositie is, de bolsector EDAB zo te kiezen dat geldt:
Inhoud(EDAB) : Inhoud(EDCB) = FH : HG,
waarbij FG een gegeven lijnstuk is dat gesneden is in H.

Stevins aanpak is op het eerste gezicht bijna onwaarschijnlijk simpel: kies het punt I op de middellijn AC zodanig dat:
(**) AI : IC = FH : HG,
en de bijbehorende bolsector EDAB is precies de gezochte.

Stevins bewijs voor deze bewering bestaat uit twee stappen:
(1) AI : IC = Oppervlakte(DAB) : Oppervlakte(DCB)
(2) Oppervlakte(DAB) : Oppervlakte(DCB) = Inhoud(EDAB) : Inhoud(EDCB)
Hierbij is met oppervlakte steeds de manteloppervlakte bedoeld, dus een bepaald deel van de bolrand. (Stevin noemt dit het clootvlack.)

Waarom is dit zo? Bewering (2) volgt uit Stevins aanpak in propositie 25 van boek 2. Volgens zijn berekening in die propositie geldt:
Inhoud(EDAB) = ¹/₃ × r × Oppervlakte(DAB),

waarbij r de straal van de bol ABCD is.
Voor een gegeven bol (met r vast) is de inhoud van elke bolsector blijkbaar evenredig met zijn manteloppervlakte, zodat (2) inderdaad waar is.

Het bewijs staat in Archimedes' boek Over de bol en de cilinder, volgens Stevin onder propositie 42 van boek 1. [Archimedes 1922] is een Duitse vertaling van dit boek, [Archimedes 2004] een Engelse. De nummers van de proposities in Stevins verwijzingen naar dit boek wijken soms af van die in de (beide) vertalingen. In propositie I.44 bewijst Archimedes dat (enigszins vrij vertaald) de inhoud van een bolsector gelijk is aan die van een kegel met het grondvlak gelijk aan de manteloppervlakte van de bolsector, en de hoogte gelijk aan de straal van de bol. (Zie: [Archimedes 2004, pp. 179-181] of [Archimedes 1922, pp. 58-60].) Dit rechtvaardigt Stevins berekening in propositie 25 van boek 2.

Bewering (1) volgt eveneens uit Archimedes' boek. In Stevins propositie 19 van boek 2 gebruikt hij de volgende relatie om de manteloppervlakte van een deel van een bol uit te rekenen:
Oppervlakte(DAB) = pi × DA²,
waarbij DA een (niet-getekend) lijnstuk in de bovenstaande afbeelding is.
Dit bewijst Archimedes volgens Stevin in propositie 40 en 41 van boek 1 van Over de bol en de cilinder. Een combinatie van I.42 en I.43 uit de vertalingen ([Archimedes 1922, pp. 56-58] en [Archimedes 2004, pp. 174-178]) geeft inderdaad dat de manteloppervlakte van DAB gelijk is aan de oppervlakte van een cirkel met straal DA.

Om van deze relatie naar (1) te komen is nog iets anders nodig. Propositie 35 van boek 3 van de Elementen van Euclides (zie [Euclid 1956, II, pp. 71-73]) zegt dat in de bovenstaande tekening geldt: DI × IB = AI × IC.
Omdat DI = IB, kunnen we ook schrijven: DI² = AI × IC.
Met behulp van de stelling van Pythagoras volgt hieruit:
DA² = AI² + DI² = AI² + AI × IC = AI × (AI + IC) = AI × AC,
en, analoog:
DC² = IC × AC.
Hiermee kunnen we inderdaad bewering (1) uit Archimedes afleiden:
Oppervlakte(DAB) : Oppervlakte(DCB) = DA² : DC² = AI : IC.

(1) en (2) zijn hiermee bewezen. En inderdaad, als we (1) en (2) combineren met (**), volgt meteen dat:
Inhoud(EDAB) : Inhoud(EDCB) = FH : HG.
Stevins methode is dus correct.

De bewijzen voor Archimedes' proposities zijn na te lezen in [Archimedes 1922] en [Archimedes 2004], en worden hier kortheidshalve niet behandeld. (Het bewijs van de afzonderlijke proposities is niet eens zo lang. Het probleem is eerder de hechte structuur van Archimedes' boek, waardoor voor goed begrip van het bewijs van bijvoorbeeld propositie 44, eigenlijk eerst de drieënveertig voorafgaande proposities moeten worden gelezen...)

Een modern bewijs is mogelijk door een coördinatenstelsel te introduceren en dan de inhoud van de bolsector te bepalen door integratie. Beide technieken waren in Stevins tijd nog niet uitgevonden. Het onderstaande bewijs geven we dan ook alleen voor de volledigheid.

Bewering: Als het punt I zo gekozen wordt dat AI = a × AC, dan geldt ook: Inhoud(EDAB) = a × Inhoud(ABCD).
(Hierbij is a een getal uit het interval [0, ½].)

Bewijs: Noem de straal van de bol r, dan is AC = 2r en dus AI = 2ar. Verder is EI = r – AI = r(1 – 2a). Uit de stelling van Pythagoras volgt dat DI² = ED² – EI² = r² – r²(1 – 4a + 4a²) = 4a(1 – a)r².
Zoals eerder gezegd bestaat de bolsector EDAB uit twee delen: een boltop (noem deze V) en de kegel EDIB. We zullen van beide afzonderlijk de inhoud bepalen, te beginnen met V.
Voer een (x,y,z)-coördinatenstelsel in met de oorsprong in E, het middelpunt van de bol. Het grondvlak van de boltop is een cirkel met straal DI, en op de z-as wordt de boltop ingesloten tussen het punt I (met coördinaten (0,0,EI)) en het punt A (met coördinaten (0,0,r). Met behulp van de eerder gevonden uitdrukkingen kunnen we V beschrijven in een stelsel ongelijkheden:

Vervolgens bepalen we de inhoud van V met een drievoudige integraal over het zojuist geparametriseerde gebied:

Deze dubbele integraal wordt eenvoudiger als we overstappen op poolcoördinaten (ρ,θ), waarbij:

Dit geeft:

Gebruik nu dat r² – 4a(1 – a)r² = (r – 2ar)²:

De inhoud van de kegel EDIB wordt eenvoudiger berekend met ¹/₃ × grondvlak × hoogte. Het grondvlak is de cirkel DBI, met straal DI, en de hoogte is EI. Beide lijnstukken hadden we al uitgedrukt in r en a, zodat meteen volgt:

De inhoud van de bolsector EDAB tenslotte, is de som van V en EDIB:

En dus geldt inderdaad: Inhoud(EDAB) = a × Inhoud(ABCD). [QED]

In de slotopmerking Merckt staat een drukfout: "int merck van 16 voorstel deses 5 boucx" moet zijn "int merck van 15 voorstel deses 5 boucx".