Tweede deel des sesten boucx van tverkeeren der vlacken

Voorstel 5: Een vierhouckich rechthouck te teyckenen van begheerde langde, ende even an een ghegheven rechthouck.
In deze propositie maakt Stevin bij een bekende rechthoek ABCD een nieuwe rechthoek met dezelfde oppervlakte, waarvan de lengte EF is voorgeschreven. Als breedte FG neemt hij de vierde evenredige van EF, AB en AD. Dat wil zeggen, er geldt:
(*) EF : AB = AD : FG.
Via kruislings vermenigvuldigen volgt dan inderdaad:
Oppervlakte(ABCD) = AB × AD = EF × FG = Oppervlakte(EFGH).

Stevin vermeldt dit niet, maar verwijst naar propositie 14 van boek 6 van Euclides' Elementen:
[Euclid 1956, II, p. 216] In equal and equiangular parallelograms the sides about the equal angles are reciprocally proportional; and equiangular parellelograms in which the sides about the equal angles are reciprocally proportional are equal.
Een rechthoek is een parallellogram waarvan alle hoeken 90° zijn, dus het tweede lid van Euclides' propositie is inderdaad een bewijs van Stevins methode: de rechthoekszijden in (*) zijn "omgekeerd evenredig".

Voorstel 6: Een viercant te teyckenen even an een ghegeven rechthouck.
ABCD is weer een gegeven rechthoek, en ditmaal moet er een vierkant worden geconstrueerd met dezelfde oppervlakte. Stevin bepaalt de middelevenredige van AB en AD. Dit is het lijnstuk EF waarvoor geldt:
(**) AB : EF = EF : AD.
Wederom geeft kruislings vermenigvuldigen: AB × AD = EF²,
waaruit meteen volgt dat het vierkant met zijde EF precies het gezochte is.

Propositie 14 van boek 2 van de Elementen, waarnaar Stevin verwijst, luidt:
[Euclid 1956, I, p. 409] To construct a square equal to a given rectilineal figure.

Toch is deze verwijzing niet helemaal juist, want Euclides gebruikt in de uitwerking van propositie 14 van boek 2 nergens de middelevenredige, maar een andere methode. Geen wonder: de middelevenredige voert hij pas in in propositie 13 van boek 6. Stevin had daarom beter kunnen verwijzen naar propositie 17 van boek 6 van de Elementen:
[Euclid 1956, II, p. 228] If three straight lines be proportional, the rectangle contained by the extremes is equal to the square on the mean; and, if the rectangle contained by the extremes be equal to the square on the mean, the three straight lines will be proportional.
Deze zegt precies wat Stevin wil: dat als (**) geldt, het vierkant EFGH en de rechthoek ABCD dezelfde oppervlakte hebben, en vice versa.

Voorstel 7: Een rechthouckich vierhouck te teyckenen van begheerde langde ende even an een ghegeven driehouck.
Bij een bekende driehoek ABC en een bekend lijnstuk DE moet een rechthoek DEGH getekend worden die dezelfde oppervlakte heeft als ABC en waarvan DE de lengte is. Stevin bepaalt eerst AF, de hoogte van de driehoek, en vervolgens de vierde evenredige van DE, ½×CB en AF, die hij EG noemt. Er geldt dus:
DE : ½CB = AF : EG,
en kruislings vermenigvuldigen levert inderdaad op:
Oppervlakte(DEGH) = DE × EG = ½ × CB × AF = Oppervlakte(ABC).

Stevin verwijst voor het bewijs naar Euclides' propositie 44 van boek 1 van de Elementen:
[Euclid 1956, I, p. 341] To a given straight line to apply, in a given rectilineal angle, a parallelogram equal to a given triangle.
Hier geldt net als in de vorige propositie dat Euclides' methode anders is dan die van Stevin. (De vierde evenredige wordt pas in boek 6 van de Elementen ingevoerd.) Bovendien construeert Euclides een parallellogram: Stevin behandelt alleen het speciale geval waarbij het parallellogram hoeken van 90° heeft en dus een rechthoek is.

Voorstel 8: Een rechthouckich vierhouck te teyckenen van begheerde langde, ende even an een ghegeven rechtlinich plat.
Gegeven zijn een willekeurige vierhoek ABCD en een rechte lijn EF, waarop een rechthoek moet worden getekend die dezelfde oppervlakte heeft als ABCD. De vierhoek wordt met een diagonaal in twee driehoeken gedeeld, en op beide driehoeken afzonderlijk past Stevin de vorige propositie toe. Dit levert twee rechthoeken op, die samen een grote rechthoek vormen die dezelfde oppervlakte heeft als de twee driehoeken samen, en dus als ABCD. Deze methode werkt ook voor andere veelhoeken, alleen zijn dan natuurlijk meer driehoeken nodig.

De verwijzing naar propositie 45 van boek 1 van de Elementen van Euclides is op zich correct, want deze luidt:
[Euclid 1956, I, p. 345] To construct, in a given rectilineal angle, a parallelogram equal to a given rectilineal figure.
Net als bij de vorige propositie geldt echter dat Euclides een algemener geval behandelt (namelijk de constructie van een parallellogram in plaats van persé een rechthoek) en dat zijn methode bovendien niet aansluit op die van Stevin. De verwijzing lijkt tamelijk overbodig: Stevin geeft een evident correcte toepassing van zijn vorige propositie.

Voorstel 9: Wesende ghegheven twee onghelijcke rechtlinighe platten: Een plat te teyckenen even ant een, ende ghelijck mettet ander.
De opgave is hier, bij twee bekende (ongelijkvormige) veelhoeken A en B een nieuwe veelhoek te tekenen die dezelfde oppervlakte heeft als A en gelijkvormig is met B. Stevin construeert hiertoe eerst twee rechthoeken met gelijke lengte, die dezelfde oppervlakte als A, respectievelijk B hebben, door de vorige propositie te gebruiken. Vervolgens meet hij EF, een zijde van de veelhoek B, en construeert hij het lijnstuk CD waarvoor geldt:
Oppervlakte(B) : Oppervlakte(A) = EF : CD.
Tenslotte bepaalt hij GH, de middelevenredige van EF en CD, dat wil zeggen:
EF : GH = GH : CD.
Hij tekent vanuit de zijde GH een veelhoek I die gelijkvormig is met B, waarbij GH uiteraard de rol van EF overneemt. (Dit gelijkvormige tekenen heeft Stevin uitgebreid behandeld propositie 16 van boek 1.)

Per constructie is I gelijkvormig met B, dus er rest alleen nog te bewijzen dat I en A dezelfde oppervlakte hebben. Stevins bewijs begint met de opmerking dat EF, GH en CD in ghedeurighe everedenheyt zijn. Dit is gewoon een andere manier om te zeggen dat EF : GH = GH : CD. Hieruit volgt:
EF : CD = ^EF/_GH × ^GH/_CD = (^EF/_GH)² = EF² : GH².

De oppervlakte van B is evenredig met het kwadraat van de zijde EF:
Oppervlakte(B) = k × EF²,
waarbij k een evenredigheidsconstante is. Omdat I en B gelijkvormig zijn, geldt er:
Oppervlakte(I) = k × GH²,
met dezelfde constante van evenredigheid. Uit EF : CD = EF² : GH² volgt daarom, zoals Stevin opmerkt:
EF : CD = Oppervlakte(B) : Oppervlakte(I).
Maar we hadden CD juist geconstrueerd zodat EF : CD = Oppervlakte(B) : Oppervlakte(A). Dus hebben A en I inderdaad dezelfde oppervlakte.

Bij het werken met getallen, zonder meetkundige constructies, heeft Prins Maurits een andere manier gevonden. Er geldt:
Oppervlakte(B) : EF² = Oppervlakte(I) : GH² ( = k),
maar Oppervlakte(I) = Oppervlakte(A), dus hierin zijn alle grootheden bekend behalve GH, die daarom meteen berekend kan worden met kruislings vermenigvuldigen.

Voorstel 10: Een driehouck te teyckenen even an een ghegheven rondt.
Gegeven een cirkel ABCD met straal EC moeten we een driehoek construeren die dezelfde oppervlakte heeft. De enige moeilijkheid in deze propositie zit hem in het trekken van een rechte lijn CF die net zo lang is als de omtrek van een cirkel. Dit probleem heeft Stevin echter al behandeld in de eerste propositie van dit boek. De constructie die Stevin daar gebruikt is een toepassing van propositie 18 van Archimedes' boek Over spiralen. (Zie [Archimedes 1922a] voor de Duitse vertaling.)

Als CF eenmaal getrokken is, volgt uit de constructie direct:
Oppervlakte(ΔEFC) = ½ × EC × CF = ½ × EC × (2 × pi × EC) = pi × EC² = Oppervlakte(ABCD).
Het voorbeeld van Prins Maurits werkt precies hetzelfde als zijn corter wercking aan het einde van de vorige propositie.

Voorstel 11: Een viercant te teyckenen even an een ghegheven rondt.
Bij een cirkel ABCD met straal EC moet een vierkant getekend worden dat dezelfde oppervlakte heeft. Dit probleem, de cirkelkwadratuur, is een van de drie klassieke onopgeloste problemen uit de Griekse wiskunde. (De andere twee zijn het verdubbelen van een kubus en de trisectie van een hoek.) Alle drie bleken niet oplosbaar te zijn met klassieke meetkunde, dat wil zeggen met alleen passer en lineaal (zonder schaalverdeling). In het geval van de cirkelkwadratuur komt dit doordat het getal pi transcendent is (zie het commentaar bij propositie 8 van boek 2). De oppervlakte van de gegeven cirkel is pi × EC², dus het beoogde vierkant zou zijde EC × √pi moeten hebben, en een lijnstuk met die lengte is niet met passer en lineaal te construeren.

Stevin heeft in propositie 8 van boek 2 echter besloten om te rekenen met de benadering pi' = ²²/₇, en dan wordt het probleem opeens wél "oplosbaar". Het betreft hier natuurlijk een schijn-oplossing, want het vierkant dat Stevin construeert heeft alleen bij benadering dezelfde oppervlakte als de cirkel.

Als zijde GH voor het vierkant neemt hij de middelevenredige van de helft van de omtrek van de cirkel (F) en de straal EC:
F : GH = GH : EC,
en inderdaad volgt daaruit, met kruislings vermenigvuldigen:
GH² = F × EC = pi' × EC × EC = Oppervlakte(ABCD).

In het Vervolgh is twee keer iets weggevallen: "want deelende t'ghetal des plats vant viercant altijt deur 22, datter uyt comt is de halfmiddellijn" moet zijn "want deelende t'ghetal des plats vant viercant altijt deur 22/7, datter uyt comt is de halfmiddellijns viercant", waarbij met dat laatste dus het kwadraat van de straal van de te tekenen cirkel bedoeld is.

Voorstel 12: Een rondt te teyckenen even an een ghegheven lanckrondt.
Gegeven is een ellips (lanckrondt) ABCD, met lange as AC en korte as DB. Er moet een cirkel worden geconstrueerd met dezelfde oppervlakte als de ellips. Volgens Stevin is de diameter EF van de gezochte cirkel precies de middelevenredige van de assen AC en DB:
AC : EF = EF : DB.
Voor het bewijs verwijst hij naar de zesde propositie van Archimedes' Over conoïden en sferoïden. [Archimedes 1923] is een Duitse vertaling van dit boek. In deze propositie bewijst Archimedes (in moderne notatie) dat de oppervlakte van een ellips gelijk is aan pi × a × b, waarbij a de lengte van de halve lange as is en b de lengte van de halve korte as.

In dit voorbeeld geldt dus:
Oppervlakte(ABCD) = pi × ½AC × ½DB,
en omdat EF² = AC × DB, per constructie, volgt inderdaad dat de oppervlakte van de gevonden cirkel gelijk is aan:
pi × (½EF)² = ¼ × pi × AC × DB = Oppervlakte(ABCD).

Stevin zegt in het getallenvoorbeeld dat de ellips en de cirkel allebei een oppervlakte van "23572 (2)" hebben. Dit is de notatie voor decimale breuken uit De Thiende, waarbij (0) voor eenheden staat, (1) voor tienden, (2) voor honderdsten, enzovoort. Bedoeld is dus een oppervlakte van 235,72. Wanneer we rekenen met Stevins benadering pi = ²²/₇, vinden we echter een oppervlakte van 235 ⁵/₇ = 235,71 (afgerond).

Voorstel 13: Op een ghegheven grootste of cleynste middellijn een lanckrondt te teyckenen even an een ghegheven lanckrondt.
ABCD is wederom een ellips met lange as AC en korte as DB. Ditmaal moet de ellips worden geconstrueerd op een gegeven as EF, die dezelfde oppervlakte heeft als ABCD. Dat wil zeggen, we moeten de bijbehorende korte as GH bepalen. Volgens Stevin is GH de vierde evenredige van EF, AC en DB:
EF : AC = DB : GH.

Dat dit klopt, volgt uit Stevins werkwijze in de 15e propositie van boek 2. Daarin berekent hij de oppervlakte van ABCD door eerst de oppervlakte van een cirkel met diameter AC te nemen, en dan te stellen:
AC : DB = (pi × (½AC)²) : Oppervlakte(ABCD).
We kunnen aan beide kanten de volgorde verwisselen en een factor AC weghalen, en zien:
(***) DB = Oppervlakte(ABCD) : (pi × ¼AC).
Als we de oppervlakte van de nieuwe ellips EHFG op dezelfde manier bepalen, volgt er:
EF : GH = (pi × (½EF)²) : Oppervlakte(EHFG),
en dus:
(****) GH = Oppervlakte(EHFG) : (pi × ¼EF).

Door (***) en (****) te combineren krijgen we:
DB : GH = (EF : AC) × (Oppervlakte(ABCD) : Oppervlakte(EHFG)).
Maar GH was zo gekozen dat DB : GH = EF : AC. Dit is alleen mogelijk als de ellipsen ABCD en EHFG dezelfde oppervlakte hebben, zoals gesteld was.

Een snellere manier om dit in te zien is deze: zoals bij de vorige propositie gezegd is, is de oppervlakte van een ellips met halve lange as a en halve korte as b gelijk aan pi × a × b. Dus:
Oppervlakte(ABCD) = pi × ½AC × ½DB.
Uit EF : AC = DB : GH volgt dat AC × DB = EF × GH, en aangezien
Oppervlakte(EHFG) = pi × ½EF × ½GH
is meteen duidelijk dat de twee oppervlaktes gelijk zijn.

Voorstel 14: Wesende ghegheven twee onghelijcke lanckronden: Een derde te teyckenen, even mettet een ende ghelijck mettet ander.
Het analogon van propositie 9 van dit boek voor ellipsen. ABCD en EFGH zijn twee bekende ellipsen (lange as AC, resp. EG), en we moeten de ellips TXVY construeren die dezelfde oppervlakte heeft als ABCD en bovendien gelijkvormig is met EFGH.

Deze constructie heeft nogal wat voeten in de aarde:

• Stevin maakt allereerst twee cirkels IKLM (met diameter IL) en NOPQ (met diameter NP), waarvoor geldt:
  Oppervlakte(IKLM) = Oppervlakte(ABCD) en Oppervlakte(NOPQ) = Oppervlakte(EFGH).
  Dit is een toepassing van de 12e propositie.
• Vervolgens bepaalt hij het lijnstuk R waarvoor geldt: NP : IL = IL : R.
• Daarna het lijnstuk S met de eigenschap: NP : R = EG : S.
• Dan construeert hij het lijnstuk TV dat de middelevenredige van S en EG is: S : TV = TV : EG.
• Tenslotte tekent hij de ellips met lange as TV die gelijkvormig is met EFGH, en dit is (eindelijk) TXVY.

TXVY is per constructie gelijkvormig met EFGH. Er rest nog te bewijzen dat ABCD en TXVY dezelfde oppervlakte hebben.

• Omdat de cirkels IKLM en NOPQ dezelfde oppervlakte hebben als ABCD, resp. EFGH, geldt er:
  Oppervlakte(ABCD) : Oppervlakte(EFGH) = IL² : NP².
• Omdat EFGH en TXVY gelijkvormig zijn, volgt er:
  Oppervlakte(TXVY) : Oppervlakte(EFGH) = TV² : EG².
  (Hierbij wordt gelijkvormigheid op dezelfde manier toegepast als eerder, bijvoorbeeld in het commentaar op propositie 9.)
• Uit NP : IL = IL : R volgt onmiddellijk: R = ^IL²/_NP.
• Door vervolgens NP : R = EG : S uit te werken, vinden we: S = EG × ^R/_NP = EG × ^IL²/_NP².
• S : TV = TV : EG laat zich dan herschrijven tot: TV² = S × EG = EG² × ^IL²/_NP².
• En dus volgt er:
  Oppervlakte(TXVY) : Oppervlakte(EFGH) = ^IL²/_NP² = Oppervlakte(ABCD) : Oppervlakte(EFGH),
  dat wil zeggen: ABCD en TXVY hebben dezelfde oppervlakte.

Prins Maurits heeft een andere manier om de lengte van TV te bepalen, die geheel analoog werkt aan zijn "kortere methode" in propositie 9. Deze voldoet, zoals steeds, niet aan de eisen van de klassieke meetkunde, maar hij is wel veel praktischer. Tenslotte merkt Stevin op dat deze propositie natuurlijk ook geldt voor cirkels, omdat cirkels gewoon ellipsen zijn met twee gelijke assen.

Voorstel 15: Een driehouck te teyckenen even an een ghegheven brantsne.
ABC is een gegeven stuk van een parabool (brantsne), waarvan AC de basis is en B het toppunt. We moeten een driehoek tekenen die dezelfde oppervlakte heeft als ABC.

Deze propositie is, net als de 16e propositie van boek 2, gebaseerd op een resultaat van Archimedes, dat door Stevin echter consequent verkeerd gebruikt wordt. In propositie 24 van Archimedes' Kwadratuur van de parabool staat namelijk:
[Archimedes 1923a, p. 27] De inhoud van een paraboolsegment is ⁴/₃ van de inhoud van de driehoek, die dezelfde basis en hoogte heeft.
Om een driehoek ABD te construeren met dezelfde oppervlakte als de parabool ABC moet daarom een basis AD worden gekozen die ⁴/₃ keer zo lang als AC is. Dan geldt immers: Oppervlakte(ΔABD) = ¹/₂ × AD × hoogte = ¹/₂ × ⁴/₃ × AC × hoogte = ⁴/₃ × Oppervlakte(ΔABC) = Oppervlakte(parabool ABC).

Waar Stevin schrijft: "Ick treck AC voorwaert tot D, also dat CD even sy anden helft van AC", moet dus eigenlijk staan "Ick treck AC voorwaert tot D, also dat CD even sy an 1/3 van AC".

Het voorbeeld van Prins Maurits werkt weer op dezelfde manier als voorheen. Er geldt:
Oppervlakte(EFGHI) = k × EF²,
waarbij k een constante van evenredigheid is. Voor de gelijkvormige veelhoek KLMNO geldt daarom:
Oppervlakte(KLMNO) = k × KL²,
en dus geldt voor de verhoudingen:
Oppervlakte(EFGHI) : Oppervlakte(KLMNO) = EF² : KL².
Wanneer we eisen dat KLMNO een bepaalde oppervlakte heeft (namelijk die van de parabool), dan is van deze vier is alleen KL² onbekend, en die kan dus hieruit bepaald worden.

Voorstel 16: Wesende ghegheven een slangtrecxplat bestaende in een of meer volcommen keeren: Een rondt te teyckenen even an t'ghegheven slangtrecxplat.
ABC is een spiraal van Archimedes met één draai, waarvan AC de basislijn is. Er moet een cirkel worden geconstrueerd die dezelfde oppervlakte heeft als de spiraal. Stevin zegt dat de cirkel DFG voldoet, met straal DE zodat:
AC : DE = DE : (¹/₃AC).
Dat wil zeggen: DE² = ¹/₃AC²

Stevin verwijst naar de 25e propositie van Over spiralen van Archimedes. In de Duitse vertaling [Archimedes 1922a, p. 45] zegt propositie nummer 24 precies wat Stevin schrijft: de oppervlakte van ABC is gelijk aan een derde van de oppervlakte van de cirkel met straal AC.

Dan volgt inderdaad: Oppervlakte(DFG) = pi × DE² = ¹/₃ × pi × AC² = Oppervlakte(ABC).

Stevin verwijst nog naar een bewijs van Archimedes omtrent de verhoudingen tussen de oppervlaktes van spiralen met meer draaiingen. Dit bewijs is na te lezen in propositie 27 van [Archimedes 1922a].

Voorstel 17: Een rondt te teyckenen even ant vlack eens ghegheven cloots.
De opgave is hier, de cirkel te maken die dezelfde oppervlakte heeft als de bol ABCD met diameter AC. Volgens Stevin is dit de cirkel E met straal gelijk aan AC.

Stevin verwijst naar propositie 31 van boek 1 van Archimedes' Over de bol en de cilinder. In de Duitse en Engelse vertaling is dit propositie I.33. Daarin staat:

[Archimedes 2004, p. 144] The surface of every sphere is four times the greatest circle of the <circles> in it.
(Voor de Duitse versie, zie [Archimedes 1922, p. 44].)

Dit komt overeen met de moderne formule voor de oppervlakte van een bol met straal r: Oppervlakte = 4 × pi × r².
Hieruit volgt Stevins bewering onmiddellijk, immers:
Oppervlakte(ABCD) = 4 × pi × (½AC)² = pi × AC² = Oppervlakte(E).

Voorstel 18: Een rondt te teyckenen even ant ghegheven bultich vlack der coordsne eens cloots.
ABC is een bolsegment, met hoogte BD en grondcirkel AC. We moeten een cirkel tekenen die dezelfde oppervlakte heeft als de manteloppervlakte van ABC.

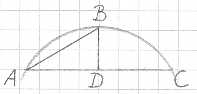Volgens Stevin is dit de cirkel met een straal ter lengte AB, en staat het bewijs van deze bewering in propositie 40 en 41 van boek I van Archimedes' Over de bol en de cilinder.

In de Duitse vertaling [Archimedes 1922, pp. 56-58] en de Engelse vertaling [Archimedes 2004, pp. 174-178] zijn dat de proposities I.42 en I.43, en daarin wordt dit inderdaad bewezen dat, in moderne formulevorm: Oppervlakte(ABC) = pi × AB².
(In propositie I.42 bewijst Archimedes de bewering voor bolsegmenten die kleiner zijn dan de helft van de oorspronkelijke bol. In propositie I.43 laat hij zien dat die beperking niet nodig is: het gestelde geldt voor alle bolsegmenten.)

Voorstel 19: Wesende ghegheuen twee onghelijcke clootscoordsneen: Een derde coordsne te teyckenen, diens bultich vlack even sy ant bultich vlack van d'een, ende ghelijck mettet bultich vlack van d'ander.
Dit is het analogon van propositie 9 (en van propositie 14) voor bolsegmenten. Er zijn twee bolsegmenten ABCD en EFGH gegeven, en er moet een derde ONMK worden gevonden die dezelfde manteloppervlakte heeft als ABCD en die gelijkvormig is met EFGH.

De constructie die Stevin hier geeft is duidelijk gebaseerd op die in propositie 6 van boek II van Over de bol en de cilinder van Archimedes, waarnaar hij verwijst. (Voor de precieze inhoud, zie [Archimedes 1922, p. 69] of [Archimedes 2004, pp. 213-216].) Op een belangrijk punt wijkt Stevin echter af van Archimedes: hij tekent het lijnstuk KM zodat het dezelfde lengte heeft als DC (zodat ONMK en ABCD dezelfde oppervlakte hebben, namelijk vanwege de vorige propositie), en stelt vervolgens dat het gevonden bolsegment tevens gelijkvormig is met EFGH. Archimedes construeert KM juist zo dat ONMK gelijkvormig is met EFGH en bewijst daaruit dat ABCD en ONMK dezelfde oppervlakte hebben. Stevins opmerking "waer af t'bewijs ghedaen is int 6 voorstel vant 2 bouck des cloots en seuls [= over de bol en de cilinder] van Archimedes" klopt dus niet helemaal.

Archimedes constructie en bewijs gaan als volgt (uitgaande van de figuur in Stevins tekst):
Om te beginnen tekent hij net als Stevin de cirkel met diameter KL zodat:
GH : DC = HI : KL.
Hij verdeelt KL in LN en NK zodat geldt:
IF : FH = LN : NK.
Hij trekt de koorde OM ter hoogte van N, en zo komt hij aan het lijnstuk KM. Dankzij IF : FH = LN : NK is het duidelijk dat ONMK en EFGH gelijkvormig zijn. Er rest dus te bewijzen dat ABCD en ONMK dezelfde oppervlakte hebben. Wegens de vorige propositie is het daarvoor voldoende om te laten zien dat DC = KM.
In plaats van IF : FH = LN : NK mogen we ook schrijven:
HI : FH = KL : NK.
Er geldt dat FH : GH = NK : KM, wegens de gelijkvormigheid van ONMK en EFGH. Door dit te combineren met HI : FH = KL : NK, vinden we:
HI : GH = KL : KM.
Door termen verwisselen volgt hieruit:
HI : KL = GH : KM.
Echter, we hadden KL zo geconstrueerd dat HI : KL = GH : DC. Dus er moet gelden: KM = DC.

Voorstel 20: Een seul te teyckenen, diens bultich vlack even sy ant vlack eens ghegheven cloots.
ABCD is een bol met diameter AC. We zoeken een cilinder die als manteloppervlakte precies de oppervlakte van ABCD heeft. Volgens Stevin is dit de cilinder waarvan zowel de hoogte als de middellijn van de grondcirkel gelijk is aan AC.

Stevin verwijst naar de 13e propositie van boek I van Archimedes' Over de bol en de cilinder:
[Archimedes 2004, p. 83] The surface of every right cylinder without the base, is equal to a circle whose radius has a mean ratio between the side of the cylinder and the diameter of the base of the cylinder.
(Voor de Duitse versie, zie: [Archimedes 1922, p. 23].) Dat wil zeggen: de manteloppervlakte van een cilinder met hoogte h en een grondcirkel met middellijn m is gelijk aan de oppervlakte van een cirkel met straal r, waarbij r de middelevenredige van h en m is: h : r = r : m.
In formulevorm betekent dit dat de manteloppervlakte gelijk is aan pi × m × h.

Voor de door Stevin geconstrueerde cilinder EFGH met hoogte EH en grondcirkel met middellijn EF, waarbij EH = EF = AC, geldt daarom:
Oppervlakte(EFGH) = pi × EF × EH = pi × AC² = 4 × pi × (½AC)² = Oppervlakte(ABCD).

N.B. In de eerste regel van Tbewijs schrijft Stevin: "T'clootvlack ABCD is even ant rondt I". Hij past hier stilzwijgend propositie 17 toe.

Voorstel 21: Een rondt te teyckenen even ant bultich vlack eens ghegheven seuls.
De werking van deze propositie is een toepassing van de letterlijke inhoud van de 13e propositie van het eerste boek van Archimedes' Over de bol en de cilinder; zie daarvoor het commentaar op de vorige propositie.

Er volgt een wat vreemde opmerking van Prins Maurits. Hij stelt eerst dat voor een cirkel met straal r geldt:
(*****) Oppervlakte(cirkel) : r² = 154 : 49.
Echter, ¹⁵⁴/₄₉ kan vereenvoudigd worden tot ²²/₇, Stevins benadering van pi. Dat is logisch, want:
Oppervlakte(cirkel) = pi × r².
De methode van de Prins is nu, dat we in (*****) voor de oppervlakte van de cirkel het gewenste getal invullen, namelijk de manteloppervlakte van de gegeven figuur (die dan natuurlijk niet persé een cilinder hoeft te zijn). Waarom hiervoor gewerkt moet worden met ¹⁵⁴/₄₉ in plaats van het gebruikelijke ²²/₇, is niet duidelijk. Misschien dat de Prins vanwege r² in (*****) in de noemer met 7² = 49 wilde werken.

Voorstel 22: Een rondt te teyckenen even an een ghegheven bultich keghelvlack.
ABC is een kegel, met een beschrijvende AB en als grondvlak een cirkel met straal BD. Er moet een cirkel worden getekend met dezelfde oppervlakte als de manteloppervlakte van ABC.

Stevins methode is (wederom) afkomstig uit Archimedes' Over de bol en de cilinder. In propositie 14 van boek I bewijst Archimedes dat (zie [Archimedes 1922, p. 25] of [Archimedes 2004, p. 91]) de manteloppervlakte van ABC gelijk is aan de oppervlakte van de cirkel met als straal de middelevenredige tussen AB en BD.
(In formulevorm betekent dat: Oppervlakte(ABC) = pi × AB × BD. In dit geval komt Archimedes' oorspronkelijke formulering echter goed van pas.)
Stevins hoeft dus alleen de middelevenredige EF van AB en BD te construeren (AB : EF = EF : BD) en vervolgens een cirkel te tekenen met straal EF.

Voorstel 23: Een rondt te teyckenen even ant bultich vlack van een ghegheven corte keghel.
Dit is een herhaling van de vorige propositie, maar nu met een afgeknotte kegel. ABCDEF is de afgeknotte kegel die ontstaat door uit de hele kegel IFD bij de top de kegel IAC te verwijderen. Er moet een cirkel getekend worden met dezelfde oppervlakte als de manteloppervlakte van ABCDEF.

Volgens Stevin is dit de cirkel met als straal de middelevenredige van AF en (AB + FE), die hij GH noemt. Dus: AF : GH = GH : (AB + FE), of te wel: GH² = AF × (AB + FE).
Dit is, zoals hij zegt, door Archimedes bewezen in Over de bol en de cilinder, echter niet in de 16e propositie van het tweede boek, maar in de 16e propositie van het eerste boek. Zie [Archimedes 1922, p. 27] of [Archimedes 2004, pp. 97-99] voor het klassieke bewijs.

Een kort modern bewijs gaat zo:
Pas de vorige propositie toe op de hele kegel IFD en de kleine kegel IAC. Dit geeft:
Oppervlakte(IFD) = pi × IF × FE,
Oppervlakte(IAC) = pi × IA × AB,
Oppervlakte(ABCDEF) = Oppervlakte(IFD) – Oppervlakte(IAC) = pi × (IF × FE – IA × AB).
Gebruik nu dat IF = IA + AF:
Oppervlakte(ABCDEF) = pi × ((IA + AF) × FE + (AF – IF) × AB) = pi × (AF × (AB + FE) + IA × FE – IF × AB).
Echter, omdat de kegels IAC en IFD gelijkvormig zijn, geldt er:
IA : AB = IF : FE,
waaruit volgt dat IA × FE – IF × AB = 0. Derhalve concluderen we:
Oppervlakte(ABCDEF) = pi × AF × (AB + FE). [QED]