Woord vooraf
Het boekje van Ludolph van Ceulen met de uitgebreide titel Kort claar bewijs dat die nieuwe ghevonden proportie eens circkels iegens zyn diameter te groot is ende ouerzulcx de quadratura circuli des zeluen vinders onrecht zy dat is "Gheprent tot Aemstelredam : by mijn Harmen Janszoon Muller / Figuersnijder / woonende inde Warmoe-straet inden vergulden Passer", heeft geen jaartal op de titelpagina staan.
Toch weten we dat het in 1585 geschreven is. Zoals Bierens de Haan [BierensdeHaan1878] heeft opgemerkt is het namelijk een reactie op Quadrature du cercle van Simon vander Eycke uit 1584, maar Van Ceulen moet het geschreven hebben voor zijn Claerder bevvys
uit 1585. Bovendien merkt Van Ceulen in Proefsteen ... [Ceulen1586] uit 1586 op: "in mijn boecxken welck tvoorleden Jaer gedruct is / hebbe ic bewesen [...]".
In 1615 het werk door de weduwe van Ludolph van Ceulen heruitgegeven als bijvoegsel bij de tweede druk van Vanden Circkel. Deze twee versies verschillen alleen wel op sommige puntenvan elkaar. In de editie van 1615 ontbreekt het voorwoord van Van Ceulen aan de lezer. Daarnaast verschilt de spelling enigszins. Het gaat weliswaar om kleinigheden, maar de titel levert al verschillen op. Zo is claar veranderd in claer, iegens in jegens en ouerzulcx in over sulcks.
Als in het commentaar geciteerd wordt, is dit uit de editie uit 1585. Deze verschilt nauwelijks van die uit 1615, maar in die editie staat consequent een s geschreven als in de editie uit 1585 een z staat. Kijk onderaan deze pagina voor de overige verschillen tussen de twee versies. In de afschriften is de oorspronkelijke spelling en interpunctie zoveel mogelijk behouden. Dat betekent dus dat er regelmatig een u staat waar we tegenwoordig een v zouden schrijven, en dat de i in plaats van de j aan het begin van een woord wordt gebruikt. Tussen vierkante haken staat mijn commentaar als letters bijvoorbeeld niet goed leesbaar zijn. Op een enkele plek merk ik op dat mijn transcripte verschilt van die van Bierens de Haan in [Bierens de Haan 1878a].
Afschrift van het voorwoord
[fol. 1.v.]
Beminde Lezer.
Gesien hebbende het Boecxken by Mr. Symon vander Eycke inden iare 84.
in druck uytgegeuen / ende den doorluchtighen Vorst den prince van Oraignien
H. M. toegeschreuen / waer [Bierens de Haan: waar] inne de voornoemde Meester Symon stelt gheuonden
te hebben de volcomen ende juyste proportie eens Circkels circonferentie iegens hare
diameter / oock om een quadraat te maken / net zoo groot zijnde als een voorgegheuen
cirkel / heeft my tzelue niet min vreemt als vermetelyck geschenen dewyle noyt eenige philosophen noch de hooghe verstandighe van aanbeghinne der werelt (datmen
weet) de voorschreuen volcomen proportie hebben connen te weghe brenghen: waar
door lust ende liefde der const my ghenodighet hebben om de waarheydt deser nieuwe
ervindinghe tondersoecken: maer het contrarie daar inne beuindende heb ic den voornoemden Symon vander Eycke zijn misgrijp by monde vriendelyck aanghedient / die
daar op andtwoordende zeer begeerde / dat ick oft yemandt anders / deze zijne inuentie zoude teghens schrijuen / ten eynde hy stoffe ende oorzake hadde de selue te verdaedighen
waar toe hy my oock naderhandt noch ernstelijck heeft doen versoecken.
Op dat het dan niet enschijne
dat ick verwaandelyck [j?] berispe zonder verbeteringe /
oft
my het verbeteren vermete zonder bewys / heb ick zonderlinghe door daanporringhe
van de voorschreuen Meester Symon zelue / oock ick ouermits myne toesegginghe / niet
connen laten cortelick te schryuen ende aan te wyzen (twelck by andere gheschictere geschictelycker had moghen off mag gedaen werden) dat de voorschreuen nieuw ervonden
propositie niet volcomen noch recht zy: waar toe my niet ghedronghen heeft yemandts haat [Bierens de Haan: haet] oft eygen eere / maer alleen des Consts
liefde / die niet en magh
lyden datmen tot de Conste onrechte ende dwalende weghen banen zoude / niet twyfelende oft de redelyck constgerighe / zal tzelue zo aanghenaam wezen / ghelyck het alleen tha-
ren besten ghedaen is door hun alder dienstwillighe
Ludolph van Cuelen [sic]
Figuren in en om een cirkel geschreven
Aan het begin van het wiskundige gedeelte van het boekje doet van Van Ceulen een aantal beweringen:
"1. Inden eersten / merckt dat alle zyden eener rechtghelijck zydiger figuere in eenen cirkel beschreuen / also dat alle winckels van dien de circonferentie raken / corter zijn dan de circonferentie des seluen circkels."
Met andere woorden: de som van alle zijden van een ingeschreven gelijkzijdige figuur, is korter dan de omtrek van de cirkel die er omheen ligt.
"2. Daer jegens alle zyden van een ghelijck rechtzydighe figuere / Die om een circkel beschreuen is / zijn langer dan de circonferentie des zeluen / twelck al ist van andere ghenoechsaem bewezen / ick na myne eenuoudighe manier aldus bewysen zal."
Van Ceulen zegt hier dat de som van alle zijden van een gelijkzijdige figuur langer is dan de omtrek van de ingeschreven cirkel. Verder merkt hij op dat dit al eerder bewezen is, maar dat hij het op een eenvoudige manier gaat bewijzen.
3. Neemt tot een exemmpel dese figuere / gheteeckent met A. daar wert gezien een cirkel met twee quadraten het een buyten omme ende dander binnen geschreuen / waar inne zyn vier diameters die den cirkel deelen / ende eenyeder quadraat in acht ghelyecke deelen."
Neem bijvoorbeeld deze figuur A.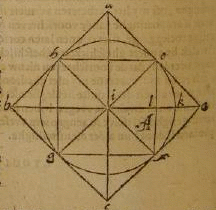 
Daarin zie je een cirkel met 2 vierkanten; een buiten de cirkel en een erbinnen geschreven. In het binnenste vierkant zie je vier diameters van de cirkel die vanuit het middelpunt I lopen naar E, F, G en H. De zijden van het vierkant worden door die lijnen in acht gelijke delen verdeeld.
"4. Dat nu de cromme linie EKF langher is dan de rechte linie ELF canmen lichtelyck bewyzen: dewijle beyde cromme ende rechte int punct E beghinnen ende in tpunct F eyndighen et cetera."
De kromme lijn EKF is langer dan de rechte lijn ELF. Van Ceulen zegt dat dit zo is omdat ze allebei in E beginnen en in F eindigen. Daamee is het dan volgens hem blijkbaar duidelijk, al doet zijn opmerking "et cetera" vermoeden dat er een of andere redenering is die hij hier niet geeft. In de editie uit 1615 van de Utrechtse UB is het "et cetera" weggelaten.
"So
dan niemandt dit can iegensspreken / volght dat den gantschen omlo[op] EFGH langer is / dan de vier zyden des quadraats inden circkel beschreuen. Item / het quadraat EDFI is grooter dan de quadrant / IKEF / welcken inhoudt geuonden werdt / alsmen de cromme linie KF multipliceert met den haluen diameter / KI"
Uit deze observaties concludeert Van Ceulen dat de omtrek van de cirkel EFGH langer is dan de vier zijden van het ingeschreven vierkant, maar korter dan de vier zijden van het omgeschreven vierkant. Hij zegt namelijk dat het vierkant EDFI groter is dan het kwadrant IKEF van de cirkel. Dit omdat de oppervlakte van het kwadrant volgens Van Ceulen gelijk is aan de lengte van EF maal EK.
Dit kun je zelf nagaan, door de kromme lijn EF te beschouwen als een deel van de omtrek van de hele cirkel. De omtrek van de hele cirkel is 2×pi×r, dus de lengte van de kromme lijn EF is EF/(2×pi×r)-de deel van de gehele omtrek. De oppervlakte van de gehele cirkel is pi×r2, dus de oppervlakte van het kwadrant is een EF/(2×pi×r)-de deel daarvan. Dat is dus EF/(2×pi×r)×pi×r2=(1/2)×EF×r. En omdat r=IK en KF=(1/2)×EF, is de oppervlakte van het kwadrant gelijk aan KF maal IK, zoals Van Ceulen ook beweert.
"Ende het inhoudt des quadraats beuindt sich alsmen multipliceert / DF met IF twelck zo langh is als / KI. Dewyle dan FD een grooter product geeft dan de cromme linie KF (als oogenschynlyck) zo
is gewis dat DF( als 1/8 der lengde aller zijden des omgescreuen quadraats) langher moet zijn als KF / twelck 1/8 is vanden ganschen omloop. Daar uyt nu lichetelyck is te besluyten dat de zijden van het viercant ABCD langher zyn / dan den omloop des in gheschreuen circkels."
De oppervlakte van het vierkant EDFI vind je door DF met IF te vermenigvuldigen , dat net zo lang is als KI. Dus DF is langer dan KF, omdat de oppervlakte die je vindt met DF×IF groter is dan die welke je vindt met KF×IF.
DF is (1/8) van de totale lengte van de zijdes van het vierkant, en KF is (1/8) van de totale omtrek van de cirkel. Op die manier bewijst Van Ceulen dat de totale lengte van de zijden van het vierkant ABCD groter is dan de omtrek van de ingeschreven cirkel.
Ingeschreven veelhoeken
"Om nu te coomen tot den handel heb ick dezen triangel ADC / etc. ghestelt. door van / DC is een 12. hoeck in een cirkel beshreven / ende den boge DEC is 1/12 van de circonferentie eens circkels wiens diameter doet 8. De zyde DC wort lichtelyck gheuonden door de 47. propositie des eersten boeck Euclidis ende is langh √24-√8 ..."
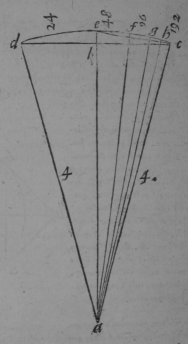
Om nu te gaan rekenen tekent Van Ceulen de driehoek ADC in een cirkel met middelpunt A. Hierin is DC de zijde van een in een cirkel geschreven 12 hoek en de boog DEC een twaalfde van de hele omtrek van de cirkel. De diameter van die cirkel stelt hij op 8. Nu kun je volgens Van Ceulen met de 47e propositie uit de elementen van Euclides, d.w.z. de stelling van Pythagoras, makkelijk uitrekenen dat de lengte van DC gelijk is aan √(24)-√(8).
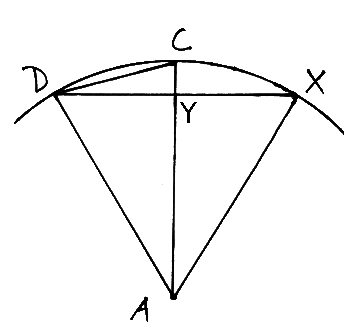Je kunt dit zelf ook doen. Kijk maar in de figuur. Daarin zie je een deel van een cirkel getekend, met daarin het lijnstuk DC, dat de zijde van een ingeschreven 12 hoek vormt. Verder staat er een punt X, dat niet in de tekening van Van Ceulen staat. Het lijnstuk DX vormt dan de zijde van een ingeschreven 6 hoek, omdat X twee keer zo ver van D af ligt, gezien langs de cirkelboog, als C. Dat betekent dat ∠DAX = 360/6 = 60o. De twee hoeken ∠ADX en ∠AXD zijn gelijk, dus die zijn allebei (180-60)/2=60o. De driehoek ADX is dus gelijkzijdig. Aangezien Van Ceulen de diameter van de cirkel op 8 heeft gesteld, is AD=4, want dat is de straal. En omdat ADX een gelijkzijdige driehoek is, is dus ook DX=4.
Laat Y het snijpunt van DX met AC. Omdat Y precies halverwege DX ligt, is DY=2 en volgens Pythagoras AY2 =AD2 - DY2=16-4=12, dus AY=√(12). Daaruit volgt dat CY=AC-AY=4-√(12), en als je nog een keer de stelling van Pythagoras toepast, zie je dat DC2 = DY2 + CY2 = 22+(4- √(12))2 = 32-8×√(12). Dus DC=√(32-8×√(12)), wat hetzelfde is als de waarde die Van Ceulen geeft: √(24)-√(8). Namelijk, (√(24)-√(8))2=32-2√(192)=32-8×√(12).
Op deze manier kun je dus uit de lengte van de zijde van een ingeschreven zeshoek die van een ingeschreven 12 hoek bepalen. Als je bovenstaande redenering toepast maar dan begint met de 12 hoek, vind je de lengte van de zijde van een ingeschreven 24 hoek. Zo verder gaand kun je de zijde van een ingeschreven 48, 96 en 192 hoek berekenen, net zoals Van Ceulen gedaan heeft.
"...voor de selue middelen vind ick de linie /EC twelck is een 24. hoeck als √.32-√384+√128 ende voor FC √.32-√.512+√98304+√32768 een 48. eck ende voor GC /comt √.32-√512+√131072+√6442450944+√2417483648. Dit is een zyde van een 96. eck / ende voor een zyde van eens 192. eck den circkels ingeschreuen als HC zal voor gewis comen √.32-√.512+√.131072+√8589934592+√27670116110564327424+√9223372036854775808 zo langh is HC."
Dat heb ik gedaan, en de waardes die ik gevonden heb, heb ik vergeleken met die van Van Ceulen. Daarbij moet je bedenken dat een punt direct na een wortelteken bij Van Ceulen betekent dat je dat wortelteken helemaal tot het einde moet doortrekken. Meer over dit soort notatie vind je in het commentaar bij Vanden Cirkel.
Zoals DC de lengte van de zijde van een ingeschreven 12-hoek is, is EC de zijde van een 24-hoek. Voor EC heb ik de waarde √(32-√(384)-√(128)) berkend, terwijl Van Ceulen als uitkomst √(32-√(384)+√(128)). Dat moet een drukfout zijn, want het blijkt dat Van Ceulen wel verdergerekend heeft met het goede getal. Voor FC, de zijde van een 48-hoek, vindt Van Ceulen namelijk √(32-√(512+√(98304)+√(32768))) en dat is hetzelfde als de waarde die ik uitgerekend heb. GC, de zijde van een 96-hoek, berekent Van Ceulen op √(32-√(512)+√(131072+√(6442450944)+√(2417483648))). Hier blijkt hij vergeten te hebben een punt te zetten na het tweede wortelteken. In onze moderne notatie wil dat zeggen dat hij het tweede wortelteken tot het einde toe door had moeten trekken. De juiste waarde noemt van Ceulen in Proefsteen: √(32-√(512)+√(131072+√(6442450944)+√(2417483648))). Deze komt overeen met het getal dat ik gevonden heb. Dit wijst erop dat het weer om een fout van de drukker gaat, temeer omdat de waarde van Van Ceulen voor HC, de zijde van een ingeschreven 192 hoek, wel klopt, namelijk. HC=√(32-√(512)+√(131072+√(6442450944)+√(2417483648))). Bekijk eventueel ook mijn berekeningen.
Overigens staat in de editie uit 1615 van Kort Claar bewijs... een drukfout in de tekening. Vergelijk beide afbeeldingen hieronder maar eens. Links staat de versie uit 1558 van de universiteitsbibliotheek van Leiden, rechts die uit 1615 van de Utrechtse UB. Van Ceulen heeft het over driehoek ADC en in de editie uit 1558 zie je die inderdaad getekend. Maar in de versie uit 1615 is punt C nergens te vinden! Op een of andere manier is het weggevallen. Je kunt aan de rechtse afbeelding meteen al zien dat er iets niet klopt, want 1/24+1/48+1/96+1/192 is niet gelijk aan 1/12, terwijl van Ceulen duidelijk zegt dat hij 1/12 cirkel getekend heeft!
Van Ceulen rekent deze getallen uit en zegt dat de diameter QM iets groter is dan 7+99892/100000 en HC iets kleiner is dan 13092/100000. Hij vermenigvuldigt dit laatste getal met 192 om de omtrek van de hele cirkel te benaderen met een omgeschreven 192 hoek en komt op 25+13664/100000. Die benadering is iets te groot, omdat zoals Van Ceulen op de eerste pagina heeft laten zien, de omtrek van een om een cirkel geschreven figuur groter is dan de omtrek van die cirkel. Dus de op die manier gevonden verhouding omtrek:diameter van (3+28497/199973) is iets te groot. Daarbij refereert hij aan wat hij in het begin bewezen heeft over de omtrek van Figuren in en om een cirkel geschreven.
Simon van der Eycke heeft volgens Van Ceulen gezegd dat een cilrkel met een diameter van 484 een omtrek heeft van "min noch meer", dwz precies 1521. Dat geeft een verhouding omtrek:diameter van 1521/484 = 3+69/484. Maar we hebben gezien dat 3+28497/199973 al te groot is, terwijl 3+69/484 zelfs nog 5589/9678932 groter is dan 3+28497/199973. De bewering van Van der Eycke is dus niet waar, en hij heeft zich "grotelyck misgrypt".
Om de lengte van een zijde van een omgeschreven 192 hoek te berekenen, tekent Van Ceulen figuur QAHPC.
Stel dat de segment AHPC een 192ste deel van een cirkel is met halve diameter 4, dwz AP=4 en HC is het getal dat we eerder uitgerekend hebben. Van Ceulen laat NMO de een boog zijn die HC raakt in punt M, zodat NMO een deel is van een cirkel met middelpunt A. Dat laatste zegt Van Ceulen er overigens niet expliciet bij, maar hij gebruikt het wel. Dan is HMC de zijde van een omgeschreven 192 hoek, met onbekende straal MA. Maar MA2=HA2-HM2, met HA=4 en HM=(1/2)×HC en HC heeft Van Ceulen op de vorige pagina bepaald. Tenslotte is de diameter gelijk aan 2 maal MA, dus op die manier vindt hij voor de diameter van de ingeschreven cirkel het getal √(32+√(512+√(131072+√(8589934592+√(27670116110564327424)+√(9223372036854775808))))).